1162、地图分析
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的所有的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
示例 1:
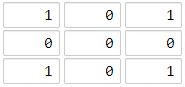
输入:[[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大,最大距离为 2。
示例 2:
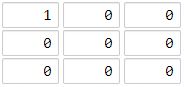
输入:[[1,0,0],[0,0,0],[0,0,0]]
输出:4
解释:
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大,最大距离为 4。
提示:
1 <= grid.length == grid[0].length <= 100grid[i][j]不是 0 就是 1
链接:https://leetcode-cn.com/problems/as-far-from-land-as-possible
题解
图论题目。
1、BFS-宽度有限搜索

class Solution {
// 位移辅助变量
int[] dx = new int[]{-1,0,1,0};
int[] dy = new int[]{0,1,0,-1};
int MAX_N = 100 + 5;
class Coordinate {
int x;
int y;
int step;
public Coordinate(int x,int y,int step) {
this.x = x;
this.y = y;
this.step = step;
}
}
int n;
// 浅拷贝
int[][] a;
boolean[][] vis;
private int findNearestLand(int x,int y) {
vis = new boolean[MAX_N][MAX_N];
Queue<Coordinate> q = new LinkedList<Coordinate>();
q.offer(new Coordinate(x,y,0));
vis[x][y] = true;
while (!q.isEmpty()) {
Coordinate f = q.peek();
q.poll();
for (int i = 0;i < 4;i++) {
int nx = f.x + dx[i],ny = f.y + dy[i];
// 遇到地图边界,直接返回
if (!(nx >= 0 && nx <= n - 1 && ny >= 0 && ny <= n -1)) {
continue;
}
// 当前位置没有被访问过
if (!vis[nx][ny]) {
q.offer(new Coordinate(nx,ny,f.step + 1));
vis[nx][ny] = true;
// 是陆地,结束。找到了最近的陆地。
if (a[nx][ny] == 1){
return f.step + 1;
}
}
}
}
return -1;
}
public int maxDistance(int[][] grid) {
this.n = grid.length;
a = grid;
int ans = -1;
for (int i = 0;i < n;i++) {
for (int j = 0;j < n;j++) {
if(a[i][j] == 0) {
ans = Math.max(ans,findNearestLand(i,j));
}
}
}
return ans;
}
}
2、多源最短路
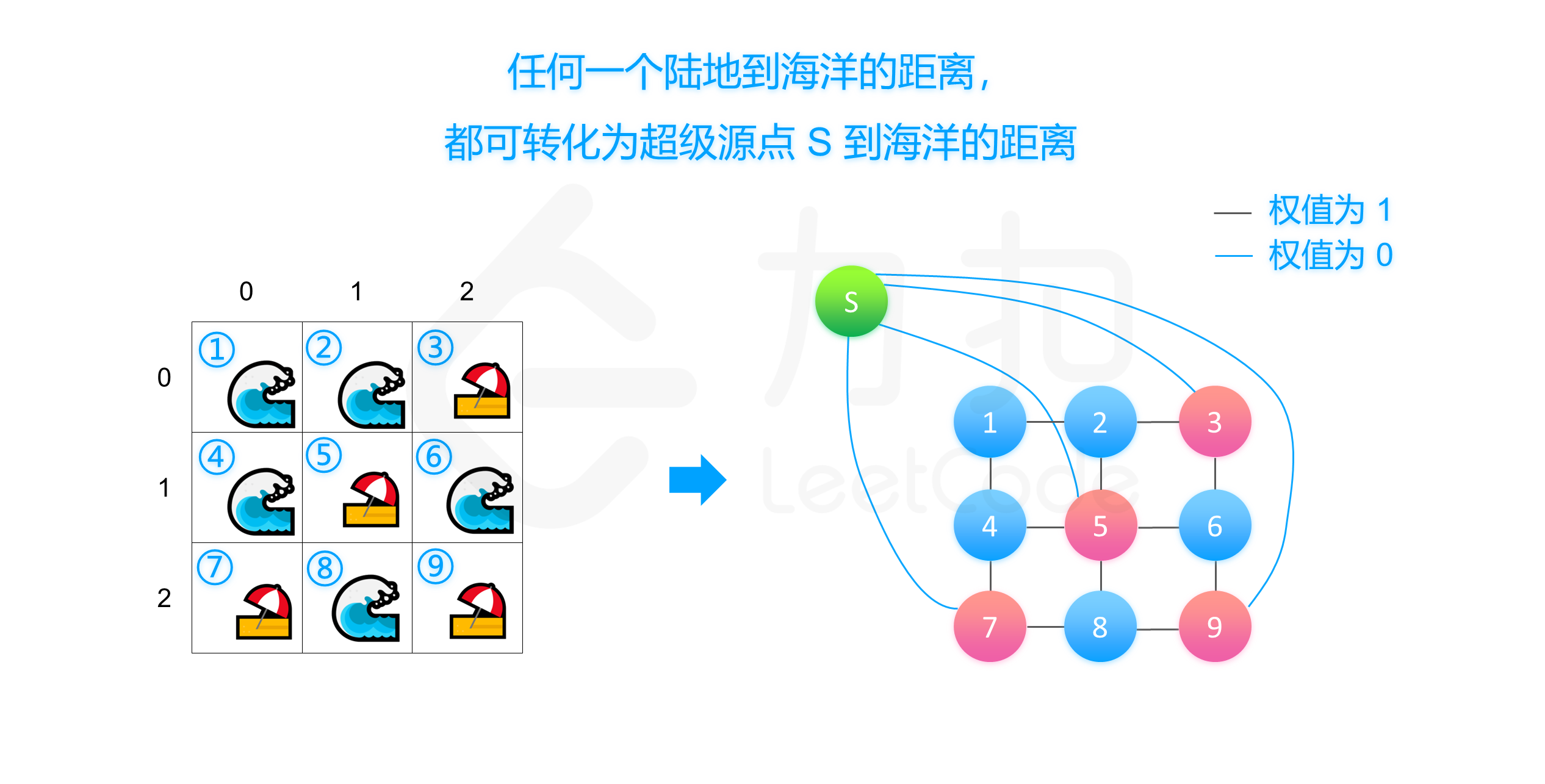
- Dijkstra版本
class Solution {
int MAX_N = 100 + 5;
int INF = 1000000;
// 位移辅助变量
int[] dx = new int[]{-1,0,1,0};
int[] dy = new int[]{0,1,0,-1};
int n;
int[][] d = new int[MAX_N][MAX_N];
class Status implement Comparable<Integer> {
int v,x,y;
public Status(int v,int x,int y) {
this.x = x;
this.y = y;
this.v = v;
}
@Override
public int compareTo(Status s2) {
return this.v - s2.v;
}
}
Queue<Status> q = new PriorityQueue<Status>();
public int maxDistance(int[][] grid) {
this.n = grid.size();
// 初始化 d数组
for (int i = 0;i < n;i++) {
for (int j = 0;j < n;j++) {
if (grid[i][j] == 1) {
d[i][j] = 0;// 陆地的距离为0
q.offer(new Status(0,i,j));
} else {
d[i][j] = INF;// 海洋距离初始化为INF
}
}
}
//
while (!q.isEmpty()) {
Status f = q.peek();
q.poll();
// 遍历四个方向
for (int i = 0;i < 4;i++) {
int nx = f.x + dx[i],ny = f.y + dy[i];
if (!(nx >= 0 && nx <= n - 1 && ny >= 0 && ny <= n - 1)) {
continue;
}
// 新位置的权值大于应该有的权值,需要更新(nx,ny)处的权值
if (f.v + 1 < d[nx][ny]) {
d[nx][ny] = f.v + 1;
q.offer(new Status(d[nx][ny],nx,ny));
}
}
}
// 遍历每一个海岸区域,求最大的距离(海洋与陆地)
int ans = -1;
for (int i = 0;i < n;i++) {
for (int j = 0;j < n;j++) {
if (grid[i][j] == 0) {
ans = Math.max(ans,d[i][j]);
}
}
}
return (ans == INF)? -1 : ans;
}
}
- 多源BFS版本
class Solution {
int MAX_N = 100 + 5;
int INF = 1000000;
// 位移辅助变量
int[] dx = new int[]{-1,0,1,0};
int[] dy = new int[]{0,1,0,-1};
int n;
int[][] d = new int[MAX_N][MAX_N];
class Coordinate {
int x, y;
public Coordinate(int x,int y) {
this.x = x;
this.y = y;
}
};
queue <Coordinate> q = new LinkedList<Coordinate>();
boolean[][] inq = new boolean[MAX_N][MAX_N];
int maxDistance(int[][] grid) {
this.n = grid.length;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
d[i][j] = 0;
q.offer(new Coordinate(i, j));
inq[i][j] = true;
} else {
d[i][j] = INF;
}
}
}
while (!q.isEmpty()) {
Coordinate f = q.peek(); q.poll(); inq[f.x][f.y] = false;
for (int i = 0; i < 4; ++i) {
int nx = f.x + dx[i], ny = f.y + dy[i];
if (!(nx >= 0 && nx <= n - 1 && ny >= 0 && ny <= n - 1)) continue;
if (d[nx][ny] > d[f.x][f.y] + 1) {
d[nx][ny] = d[f.x][f.y] + 1;
if (!inq[nx][ny]) {
q.offer(new Coordinate(nx, ny));
inq[nx][ny] = true;
}
}
}
}
int ans = -1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) ans = Math.max(ans, d[i][j]);
}
}
return (ans == INF) ? -1 : ans;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/as-far-from-land-as-possible/solution/di-tu-fen-xi-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3、动态规划
考虑优化方法二中的「把陆地区域作为源点集、海洋区域作为目标点集,求最短路」的过程。我们知道对于每个海洋区域 (x, y)(x,y),离它最近的陆地区域到它的路径要么从上方或者左方来,要么从右方或者下方来。考虑做两次动态规划,第一次从左上到右下,第二次从右下到左上,记 f(x, y) 为 (x,y) 距离最近的陆地区域的曼哈顿距离。
- 第一阶段:从左上到右下
$$
f(x,y)=\begin{cases}
0,& (x,y)是陆地\
min{f(x-1,y),f(x,y-1)}+1, & (x,y)是海洋
\end{cases}
$$ - 第二阶段:从右下到左上
$$
f(x,y)=\begin{cases}
0,& (x,y)是陆地\
min{f(x+1,y),f(x,y+1)}+1, &(x,y)是海洋
\end{cases}
$$
class Solution {
int MAX_N = 100 + 5;
int INF = 1000000;
int[][] f = new int[MAX_N][MAX_N];
int n;
int maxDistance(int[][] grid) {
this.n = grid.length;
// 初始化状态数组
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
f[i][j] = (a[i][j] == 1 ? 0 : INF);
}
}
// 从左上到右下
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) continue;
if (i - 1 >= 0) f[i][j] = Math.min(f[i][j], f[i - 1][j] + 1);
if (j - 1 >= 0) f[i][j] = Math.min(f[i][j], f[i][j - 1] + 1);
}
}
// 从右下到左上
for (int i = n - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
if (grid[i][j] == 1) continue;
if (i + 1 < n) f[i][j] = Math.min(f[i][j], f[i + 1][j] + 1);
if (j + 1 < n) f[i][j] = Math.min(f[i][j], f[i][j + 1] + 1);
}
}
int ans = -1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
ans = Math.max(ans, f[i][j]);
}
}
}
if (ans == INF) return -1;
else return ans;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/as-far-from-land-as-possible/solution/di-tu-fen-xi-by-leetcode-solution/
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

