使用 oh-my-zsh

119、杨辉三角II

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

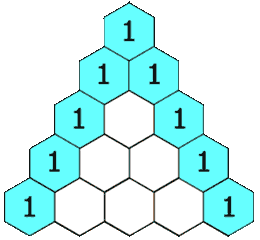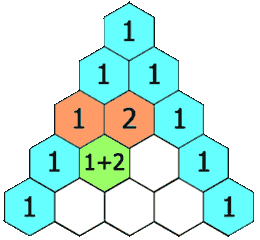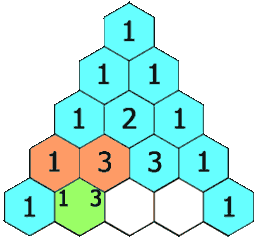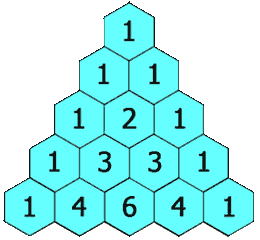
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

题解

1、模拟计算

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        
        for (int i = 1;i <= rowIndex+1;i++) {
            List<Integer> tmp = new ArrayList<>();
            if (i <= 2) {
                for (int j = 0;j < i;j++) {
                    tmp.add(1);
                }
                res.add(tmp);
            } else {
                tmp.add(1);
                List<Integer> tmp0 = res.get(i-2);
                for (int j = 1;j < i-1;j++) {
                    tmp.add(tmp0.get(j-1)+tmp0.get(j));
                }
                tmp.add(1);
                res.add(tmp);
            }
        }
        return res.get(rowIndex);
    }
}

• 空间复杂度$O(k)$

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> res = new ArrayList<>(rowIndex);
        res.add(1);
        // 求每一行
        for (int i = 1;i <= rowIndex;i++) {
            // 记录初始值
            int pre = 1;
            // 更新到第i行
            for (int j = 1;j < i;j++) {
                int tmp = pre;
                pre = res.get(j);
                res.set(j,pre+tmp);
            }
            res.add(1);
        }
        return res;
    }
}

// 从后往前推倒
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> res = new ArrayList<>(rowIndex);
        // 求每一行
        for (int i = 1;i <= rowIndex;i++) {
            // 记录初始值
            res.add(1);
            // 更新到第i行
            for (int j = i-1;j > 0;j--) {
                res.set(j,res.get(j-1)+res.get(j));
            }
        }
        res.add(1);
        return res;
    }
}

公式计算

对于第k行，的第i个元素：
$a[i] = pre*(N - i + 1)/i,0<i≤N,pre前一个元素，N第几行。$

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> ans = new ArrayList<>();
    int N = rowIndex;
    long pre = 1;
    ans.add(1);
    for (int k = 1; k <= N; k++) {
        long cur = pre * (N - k + 1) / k;
        ans.add((int) cur);
        pre = cur;
    }
    return ans;
    }
}

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com