1、 拿硬币
题目难度Easy
桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。
示例 1:
输入:[4,2,1]
输出:4
解释:第一堆力扣币最少需要拿 2 次,第二堆最少需要拿 1 次,第三堆最少需要拿 1 次,总共 4 次即可拿完。
示例 2:
输入:[2,3,10]
输出:8
限制:
1 <= n <= 41 <= coins[i] <= 10
题解
1、累加每个元素除以2的商和余数
- 代码
// java
class Solution {
public int minCount(int[] coins) {
int res = 0;
for (int i = 0;i<coins.length;i++) {
res += coins[i]/2+coins[i]%2;
}
return res;
}
}
2. 传递信息
题目难度Easy
小朋友 A 在和 ta 的小伙伴们玩传信息游戏,游戏规则如下:
有 n 名玩家,所有玩家编号分别为 0 ~ n-1,其中小朋友 A 的编号为 0
每个玩家都有固定的若干个可传信息的其他玩家(也可能没有)。传信息的关系是单向的(比如 A 可以向 B 传信息,但 B 不能向 A 传信息)。
每轮信息必须需要传递给另一个人,且信息可重复经过同一个人
给定总玩家数 n,以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数;若不能到达,返回 0。
示例 1:
输入:n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3
输出:3
解释:信息从小 A 编号 0 处开始,经 3 轮传递,到达编号 4。共有 3 种方案,分别是 0->2->0->4, 0->2->1->4, 0->2->3->4。
示例 2:
输入:n = 3, relation = [[0,2],[2,1]], k = 2
输出:0
解释:信息不能从小 A 处经过 2 轮传递到编号 2
限制:
2 <= n <= 101 <= k <= 51 <= relation.length <= 90, 且 relation[i].length == 20 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]
题解
1、图论,深度优先搜索与广度优先搜索
- 深度优先搜索
class Solution {
int count;
public int numWays(int n, int[][] relation, int k) {
count = 0;
// 邻接表
Map<Integer,List<Integer>> map = new HashMap<>();
// 初始化邻接表
for(int[] re : relation) {
if(map.containsKey(re[0])){
map.get(re[0]).add(re[1]);
}else{
List<Integer> list = new ArrayList<>();
list.add(re[1]);
map.put(re[0],list);
}
}
// 深度优先搜索递归实现
dfs(map,0,k,n);
return count;
}
// 深度优先搜索递归实现
private void dfs(Map<Integer,List<Integer>> map,int next,int k,int n){
// 到达目标位置 且 只使用了k步
if (next == n - 1 && k == 0){
count++;
return;
}
// 超过了k步
if (k < 0){
return;
}
// 递归调用
List<Integer> list = map.get(next);
// 该位置无法传递
if (list != null) {
for(int a : list) {
dfs(map,a,k-1,n);
}
}
}
}
- 广度优先搜索
class Solution {
public int numWays(int n, int[][] relation, int k) {
// 该需要一个变量统计总次数是否为k
// 是返回值错了,而不是超时,考虑一些特殊情况
// 现将relation数组按第一个元素从小到大排序
Arrays.sort(relation, (v1, v2) -> v1[0] - v2[0]); // 第一项为0的项都在最前面
int res = 0; // 返回值 方案数
int N = relation.length;
int depth = 0;
int len = 0;
Queue<int[]> queue = new LinkedList<int[]>();
for(int i = 0; i < N; i++) {
if(relation[i][0] == 0) {
len++;
}
}
// 传递信息只从编号0开始,不是从每一个节点开始
for(int i = 0; i < len; i++) { // 逐个元素进行广搜?肯定有重复
// queue.clear(); // 清空queue 防止上一轮遍历结尾元素的干扰
queue.clear();
depth = 0; // depth没更新,所以后面的元素进不来
queue.offer(relation[i]); // 从0开始逐个元素搜索
while(!queue.isEmpty()) { // 最终肯定是要把所有入队元素都poll出去的 为空就代表广度遍历完成
int size = queue.size(); // 当前层元素总数
depth++; // 有一层元素就加1,所以先加加
if(depth > k) { // 如果此时遍历层数大于k了,后面肯定都没机会了
break; // 但是queue中此时可能还有没出队的元素,在下一轮循环之前需要清空queue
}
for(int j = 0; j < size; j++) { // 每次poll出的个数为当前size数,poll完push的在下一层计算
int[] temp = queue.poll();
int cur = temp[0];
int next = temp[1];
if(depth == k && next == n - 1) { // 如果为第k层且next等于n-1
res++; // 返回值+1
}
// 决定下一层数组中谁入队
for(int l = 0; l < N; l++) { // 可能可以从后往前连起来?depth超过k还找不到就直接跳出了
if(relation[l][0] == next) { // 如果首元素和next相等
queue.offer(relation[l]);
}
}
}
}
}
return res;
}
}
// 作者:Yokka
// 链接:https://leetcode-cn.com/problems/chuan-di-xin-xi/solution/java-bfs-by-yokka/
3、离散数学,计算可达矩阵
计算可达矩阵,也就是邻接矩阵的k次幂,用快速幂做矩阵快速幂,然后mat[0][n-1]就是长度为k的路径条数。
typedef long long ll;
// 方式数值溢出
const ll mod = 1e9+7;
// 矩阵数据结构
struct node {
ll mat[15][15];//定义矩阵
}x,y;
int len;
node mul(node x,node y){//矩阵乘法
node tmp;
for(int i=0;i<len;i++){
for(int j=0;j<len;j++){
tmp.mat [i][j]=0;
for(int k=0;k<len;k++){
tmp.mat [i][j]+=(x.mat [i][k]*y.mat [k][j])%mod;
}
tmp.mat [i][j]=tmp.mat[i][j]%mod;
}
}
return tmp;
}
node matpow(node x,node y,int num){//矩阵快速幂
while(num){
if(num&1){
y=mul(y,x);
}
x=mul(x,x);
num=num>>1;
}
return y;
}
class Solution {
public:
int numWays(int n, vector<vector<int>>& relation, int k) {
node x,res;
len = n;
memset(x.mat,0,sizeof(x.mat));
for(auto& e:relation){
x.mat[e[0]][e[1]] = 1;
}
res = matpow(x,x,k-1);
return res.mat[0][n-1];
}
};
// 作者:sinclairwang
// 链接:https://leetcode-cn.com/problems/chuan-di-xin-xi/solution/chi-san-shu-xue-ji-suan-ke-da-ju-zhen-by-sinclairw/
2、动态规划
状态解释:
dp[i][j]表示第i轮传递信息,到达j的总方案数量。
class Solution {
public int numWays(int n, int[][] relation, int k) {
int[][] dp = new int[6][10];
// 初始值,表示第0轮到达0只有一种方案
dp[0][0] = 1;
for(int i = 0;i < k;i++) {
for (int[] r : relation) {
dp[i+1][r[1]] += dp[i][r[0]];
}
}
return dp[k][n-1];
}
}
3、 剧情触发时间
题目难度Medium
在战略游戏中,玩家往往需要发展自己的势力来触发各种新的剧情。一个势力的主要属性有三种,分别是文明等级(C),资源储备(R)以及人口数量(H)。在游戏开始时(第 0 天),三种属性的值均为 0。
随着游戏进程的进行,每一天玩家的三种属性都会对应增加,我们用一个二维数组 increase 来表示每天的增加情况。这个二维数组的每个元素是一个长度为 3 的一维数组,例如 [[1,2,1],[3,4,2]] 表示第一天三种属性分别增加 1,2,1 而第二天分别增加 3,4,2。
所有剧情的触发条件也用一个二维数组 requirements 表示。这个二维数组的每个元素是一个长度为 3 的一维数组,对于某个剧情的触发条件 c[i], r[i], h[i],**如果当前 C >= c[i] 且 R >= r[i] 且 H >= h[i] **,则剧情会被触发。
根据所给信息,请计算每个剧情的触发时间,并以一个数组返回。如果某个剧情不会被触发,则该剧情对应的触发时间为 -1 。
示例 1:
输入: increase = [[2,8,4],[2,5,0],[10,9,8]] requirements = [[2,11,3],[15,10,7],[9,17,12],[8,1,14]]
输出: [2,-1,3,-1]
解释:
初始时,C = 0,R = 0,H = 0
第 1 天,C = 2,R = 8,H = 4
第 2 天,C = 4,R = 13,H = 4,此时触发剧情 0
第 3 天,C = 14,R = 22,H = 12,此时触发剧情 2
剧情 1 和 3 无法触发。
示例 2:
输入: increase = [[0,4,5],[4,8,8],[8,6,1],[10,10,0]] requirements = [[12,11,16],[20,2,6],[9,2,6],[10,18,3],[8,14,9]]
输出: [-1,4,3,3,3]
示例 3:
输入: increase = [[1,1,1]] requirements = [[0,0,0]]
输出: [0]
限制:
1 <= increase.length <= 100001 <= requirements.length <= 1000000 <= increase[i] <= 100 <= requirements[i] <= 100000
1、排序+筛选
- 代码
class Solution {
class Plot implements Comparable<Plot>{
int type;
int index;
int[] condition;
public Plot(int type,int index,int[] condition) {
this.type = type;
this.index = index;
this.condition = condition;
}
@Override
public int compareTo(Plot b){
// 从小到大排列
if (condition[0] >= b.condition[0]){
return 1;
}
return -1;
}
// @Override
// public String toString(){
// return "type: "+type+", index: "+index+", C = "+condition[0]+", R = "+condition[1]+", H = "+condition[2];
// }
}
public int[] getTriggerTime(int[][] increase, int[][] requirements) {
List<Plot> plotList = new ArrayList<>();
int i = 0;
int[] count = new int[3];
plotList.add(new Plot(1,i++,Arrays.copyOf(count,3)));
for (int[] in : increase) {
count[0] += in[0];
count[1] += in[1];
count[2] += in[2];
plotList.add(new Plot(1,i++,Arrays.copyOf(count,3)));
}
i = 0;
for (int[] re : requirements) {
plotList.add(new Plot(2,i++,Arrays.copyOf(re,3)));
}
Collections.sort(plotList);
// for(Plot p:plotList) {
// System.out.println(p);
// }
int[] res = new int[requirements.length];
for (int j = 0;j < requirements.length;j++) {
res[j] = -1;
}
List<Plot> tmp = new ArrayList<>();
for (Plot plot : plotList) {
if (plot.type == 1){
for (Plot p : tmp){
if(plot.condition[0] >= p.condition[0] && plot.condition[1] >= p.condition[1] && plot.condition[2] >= p.condition[2]) {
res[p.index] = plot.index;
}
}
tmp.clear();
} else {
tmp.add(plot);
}
}
return res;
}
}
2、二分查找
对于每一个情节,查找其是否可以触发以及触发的时机
class Solution {
public int[] getTriggerTime(int[][] increase, int[][] requirements) {
int day = 0;
int[] ans = new int[requirements.length];
//将increase中的三元组的含义变为每一天的属性值
for(int i = 1;i<increase.length;i++){
increase[i][0] += increase[i-1][0];
increase[i][1] += increase[i-1][1];
increase[i][2] += increase[i-1][2];
}
for(int i = 0;i<requirements.length;i++){
if(requirements[i][0]==0&&requirements[i][1]==0&&requirements[i][2]==0) ans[i] = 0;
else{
int left = 0;
int right = increase.length-1;
//如果最后一天仍不满足,设为-1
if(!(increase[right][0]>=requirements[i][0]&&increase[right][1]>=requirements[i][1]&&increase[right][2]>=requirements[i][2])){
ans[i] = -1;
continue;
}
//二分查找
while(left <right){
int mid = (left+right)/2;
if(!(increase[mid][0]>=requirements[i][0]&&increase[mid][1]>=requirements[i][1]&&increase[mid][2]>=requirements[i][2])){
left = mid+1;
}else{
right = mid;
}
}
ans[i] = left+1;
}
}
return ans;
}
}
// 作者:Codeband
// 链接:https://leetcode-cn.com/problems/ju-qing-hong-fa-shi-jian/solution/javaer-fen-cha-zhao-by-codeband/
4、最小跳跃次数
题目难度Hard
为了给刷题的同学一些奖励,力扣团队引入了一个弹簧游戏机。游戏机由 N 个特殊弹簧排成一排,编号为 0 到 N-1。初始有一个小球在编号 0 的弹簧处。若小球在编号为 i 的弹簧处,通过按动弹簧,可以选择把小球向右弹射 jump[i] 的距离,或者向左弹射到任意左侧弹簧的位置。也就是说,在编号为 i 弹簧处按动弹簧,小球可以弹向 0 到 i-1 中任意弹簧或者 i+jump[i] 的弹簧(若 i+jump[i]>=N ,则表示小球弹出了机器)。小球位于编号 0 处的弹簧时不能再向左弹。
为了获得奖励,你需要将小球弹出机器。请求出最少需要按动多少次弹簧,可以将小球从编号 0 弹簧弹出整个机器,即向右越过编号 N-1 的弹簧。
示例 1:
输入:jump = [2, 5, 1, 1, 1, 1]
输出:3
解释:小 Z 最少需要按动 3 次弹簧,小球依次到达的顺序为 0 -> 2 -> 1 -> 6,最终小球弹出了机器。
限制:
1 <= jump.length <= 10^61 <= jump[i] <= 10000
题解
1、动态规划-自顶向下
dp[i]表示到达从n-1出到达出所需的步数。
class Solution {
public int minJump(int[] jump) {
int[] dp = new int[jump.length];
dp[jump.length-1] = 1;
for(int i=jump.length-2;i>=0;i--){
dp[i] = jump[i]+i >= jump.length?1:dp[jump[i]+i]+1;
//更新了,当前位置后可以影响的右边的dp值,如果后续位置的dp值大于当前位置才需要更新。
for(int j = i+1; j < dp.length && dp[j] > dp[i]; j++){
dp[j] = Math.min(dp[i]+1,dp[j]);
}
}
//System.out.println(Arrays.toString(dp));
return dp[0];
}
}
// 作者:dongyangliu
// 链接:https://leetcode-cn.com/problems/zui-xiao-tiao-yue-ci-shu/solution/jian-dan-yi-dong-de-dong-tai-gui-hua-wan-fa-by-don/
5、 二叉树任务调度
通过的用户数80
尝试过的用户数204
用户总通过次数83
用户总提交次数322
题目难度Hard
任务调度优化是计算机性能优化的关键任务之一。在任务众多时,不同的调度策略可能会得到不同的总体执行时间,因此寻求一个最优的调度方案是非常有必要的。
通常任务之间是存在依赖关系的,即对于某个任务,你需要先完成他的前导任务(如果非空),才能开始执行该任务。我们保证任务的依赖关系是一棵二叉树,其中 root 为根任务,root.left 和 root.right 为他的两个前导任务(可能为空),root.val 为其自身的执行时间。
在一个 CPU 核执行某个任务时,我们可以在任何时刻暂停当前任务的执行,并保留当前执行进度。在下次继续执行该任务时,会从之前停留的进度开始继续执行。暂停的时间可以不是整数。
现在,系统有两个 CPU 核,即我们可以同时执行两个任务,但是同一个任务不能同时在两个核上执行。给定这颗任务树,请求出所有任务执行完毕的最小时间。
示例 1:
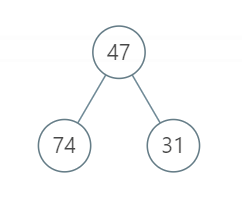
输入:root = [47, 74, 31]
输出:121
解释:根节点的左右节点可以并行执行31分钟,剩下的43+47分钟只能串行执行,因此总体执行时间是121分钟。
示例 2:
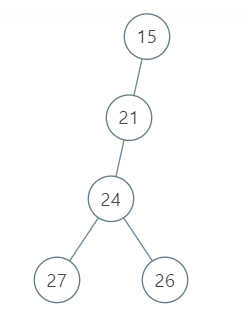
输入:root = [15, 21, null, 24, null, 27, 26]
输出:87
示例 3:
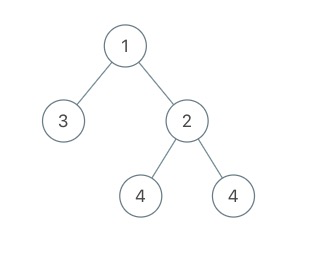
输入:root = [1,3,2,null,null,4,4]
输出:7.5
限制:
1 <= 节点数量 <= 10001 <= 单节点执行时间 <= 1000
题解
1、后序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
/**
* LCP 10. 二叉树任务调度
* @param root
* @return
*/
public double minimalExecTime(TreeNode root) {
double[] res = execTime(root,2);
return res[0];
}
/**
* 获取node最小执行时间
* @param node node
* @param n 并行数
* @return [0]执行完当前节点最小耗时,[1]当前node为根的时间串行之和
*/
private double[] execTime(TreeNode node,int n){
if (node == null){
// [0]执行完当前节点最小耗时,[1]当前node为根的时间串行之和
return new double[]{0.0D,0.0D};
}
// 获取左右子树的值
double[] leftTime = execTime(node.left,n);
double[] rightTime = execTime(node.right,n);
// 左右子树节点之和
double sum = leftTime[1] + rightTime[1];
// 当前节点执行完的最小消耗时间
double minTime = Math.max(Math.max(leftTime[0],rightTime[0]),sum/n) + node.val;
return new double[]{minTime,sum + node.val};
}
}
// 作者:burning-summer
// 链接:https://leetcode-cn.com/problems/er-cha-shu-ren-wu-diao-du/solution/hou-xu-bian-li-di-gui-fan-hui-zuo-you-zi-shu-zui-y/
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

