给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2)。
上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。
示例:
给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
说明:
- 你可以假设矩阵不可变。
- 会多次调用 sumRegion 方法。
- 你可以假设 row1 ≤ row2 且 col1 ≤ col2。
题解
1、动态规划–前缀和子矩阵
- 缓存行
- 将二维矩阵视为一维矩阵的m行
- 计算每一行的前缀和,然后根据需求求出对应的子矩阵的和
class NumMatrix {
int[][] dp;
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return;
dp = new int[matrix.length][matrix[0].length + 1];
// 求每一行的前缀和
for(int i = 0;i < matrix.length;i++) {
for (int j = 0;j < matrix[0].length;j++) {
dp[i][j+1] = dp[i][j] + matrix[i][j];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int res = 0;
for (int i = row1;i <= row2;i++) {
res += dp[i][col2+1] - dp[i][col1];
}
return res;
}
}
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* int param_1 = obj.sumRegion(row1,col1,row2,col2);
*/
- 智能缓存
- 我们在一维版本中使用了累积和数组。我们注意到累积和是根据索引 0 处的原点计算的。将这个类比扩展到二维情况,我们可以预先计算出一个与原点相关的累积区域和,即
(0,0)。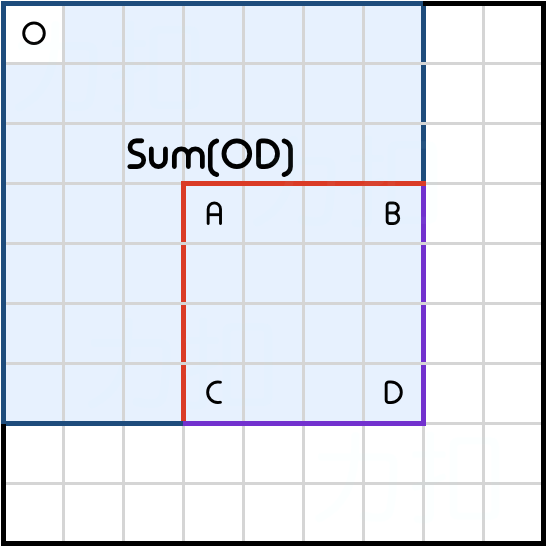
Sum(OD)是相对于原点(0,0)的累计区域和。
如何使用预先计算的累积区域和得出 Sum(ABCD) 呢?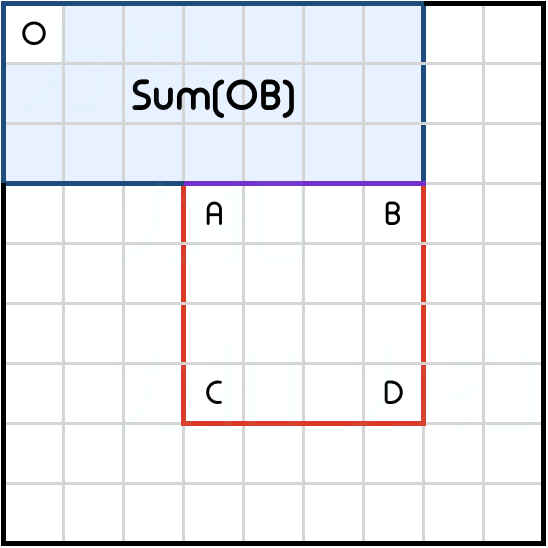
Sum(OB)是矩形顶部的累积区域和。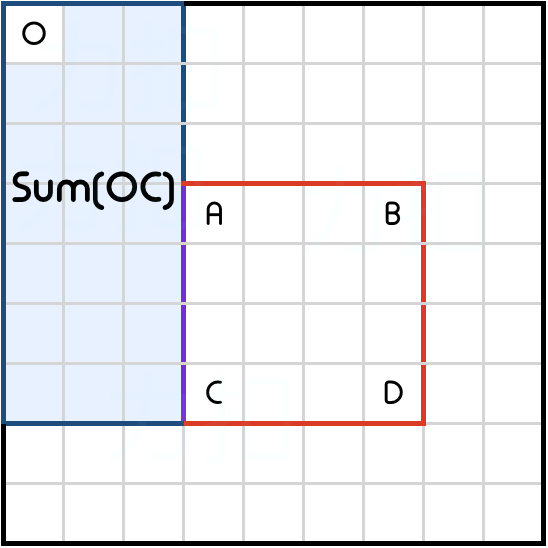
Sum(OC)是矩形左侧的累积区域和。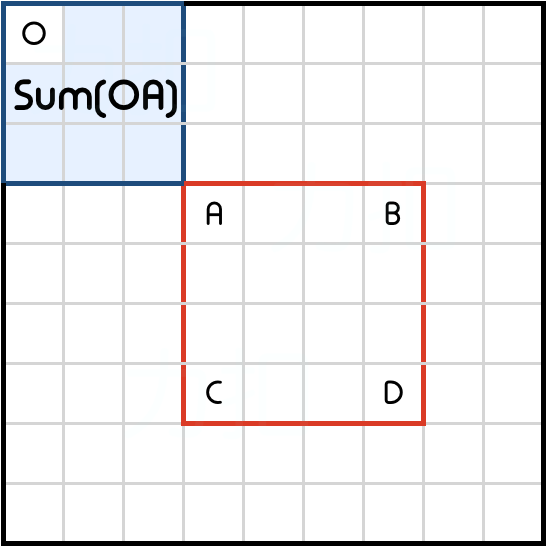
Sum(OA) 是矩形左上角的累积区域和。
区域 Sum(OA) 由 Sum(OB) 和 Sum(OC)两次覆盖。我们可以使用包含排除原则计算 Sum(ABCD) 如下:
$$ sum(abcd)=sum(od)−sum(ob)−sum(oc)+sum(oa)$$
class NumMatrix {
private int[][] dp;
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return;
// 长度多1,便于数组处理和计算
dp = new int[matrix.length + 1][matrix[0].length + 1];
// 先求(0,0)到(i,j)的前缀子矩阵和
for(int i = 0;i < matrix.length;i++) {
for (int j = 0;j < matrix[0].length;j++) {
dp[i+1][j+1] = dp[i+1][j] + dp[i][j+1] + matrix[i][j]- dp[i][j];
}
}
}
// 再求(r1,c1)到(r2,c2)的子矩阵的和
public int sumRegion(int row1, int col1, int row2, int col2) {
return dp[row2 + 1][col2 + 1] - dp[row1][col2+1] - dp[row2+1][col1] + dp[row1][col1];
}
}
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* int param_1 = obj.sumRegion(row1,col1,row2,col2);
*/
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

