n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
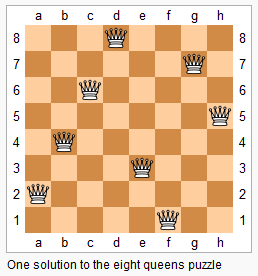
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
- 输入: 4
- 输出:
[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
官方的解
- 深度优先,递归回溯
- 数学规律
- 行列记录
rows[row] = col - 正对角线记录
row - col + 2*n - 次对角线记录
row + col - 保证正对角线与次对角线不冲突
- 行列记录
N=4
- 正对角线记录
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 8 | 7 | 6 | 5 |
| 1 | 9 | 8 | 7 | 6 |
| 2 | 10 | 9 | 8 | 7 |
| 3 | 11 | 10 | 9 | 8 |
- 次对角线记录
| X | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 3 | 4 | 5 |
| 3 | 3 | 4 | 5 | 6 |
代码
class Solution {
// 辅助变量
int rows[];// 行列占领标记 0~n
int hills[];// 正对角线占领标记 2n~4n-1
int dales[];// 次对角线占领标记 0~2n-1
int n;// 边长
// output 结果集
List<List<String>> output = new ArrayList<List<String>>();
int queens[];// 记录皇后的位置
// 判断当前位置是否会被其他皇后攻击
public boolean isNotUnderAttact(int row,int col) {
int res = rows[col] + hills[row - col + 2*n] + dales[row + col];
return (res == 0) ? true : false;
}
// 在(row,col)处放置皇后
public void placeQueen(int row, int col) {
queens[row] = col;// 第row行的第col列,放上皇后
rows[col] = 1;// 第row行的第col列,占领行列
hills[row - col + 2*n] = 1;// 占领正对角线
dales[row + col] = 1;// 占领次对角线
}
// 移除(row,col)处放置的皇后
public void removeQueen(int row,int col) {
queens[row] = 0;// 移除皇后
// 状态复原
rows[col] = 0;// 第row行的第col列,释放行列
hills[row - col + 2*n] = 0;// 释放正对角线
dales[row + col] = 0;// 释放次对角线
}
// 构造某一个解
public void addSolution() {
List<String> solution = new ArrayList<String>();
// 构造每一行
for (int i = 0;i < n;i++) {
int col = queens[i];
StringBuilder sb = new StringBuilder();
for (int j = 0;j < col;j++) {
sb.append(".");
}
sb.append("Q");
for (int j = 0;j < n - col - 1;j++) {
sb.append(".");
}
solution.add(sb.toString());
}
output.add(solution);
}
// 回溯算法
public void backtract(int row){
for (int col = 0;col < n;col++) {
if (isNotUnderAttact(row,col)) {// 当前(row,col)位置没有皇后占领
placeQueen(row,col);// 放置皇后
if (row + 1 == n) {// 完成最后一行的皇后的寻找
addSolution();// 构造一个解。不需要return,需要回溯尝试其他情况
} else {// 没有结束
// 深度优先递归
backtract(row+1);
}
// 回溯
removeQueen(row,col); // 移除皇后
}
}
}
// 主方法
public List<List<String>> solveNQueens(int n) {
this.n = n;
rows = new int[n];
hills = new int[4*n - 1];
dales =
new int[2*n - 1];
queens = new int[n];
backtract(0);
return output;
}
}
52、求N皇后的解的个数
- 直接修改51题的代码,将结果改为一个整数即可
class Solution {
// 辅助变量
int rows[];// 行列占领标记 0~n
int hills[];// 正对角线占领标记 2n~4n-1
int dales[];// 次对角线占领标记 0~2n-1
int n;// 边长
// output 结果
int count = 0;
int queens[];// 记录皇后的位置
// 判断当前位置是否会被其他皇后攻击
public boolean isNotUnderAttact(int row,int col) {
int res = rows[col] + hills[row - col + 2*n] + dales[row + col];
return (res == 0) ? true : false;
}
// 在(row,col)处放置皇后
public void placeQueen(int row, int col) {
queens[row] = col;// 第row行的第col列,放上皇后
rows[col] = 1;// 第row行的第col列,占领行列
hills[row - col + 2*n] = 1;// 占领正对角线
dales[row + col] = 1;// 占领次对角线
}
// 移除(row,col)处放置的皇后
public void removeQueen(int row,int col) {
queens[row] = 0;// 移除皇后
// 状态复原
rows[col] = 0;// 第row行的第col列,释放行列
hills[row - col + 2*n] = 0;// 释放正对角线
dales[row + col] = 0;// 释放次对角线
}
// 回溯算法
public void backtract(int row){
for (int col = 0;col < n;col++) {
if (isNotUnderAttact(row,col)) {// 当前(row,col)位置没有皇后占领
placeQueen(row,col);// 放置皇后
if (row + 1 == n) {// 完成最后一行的皇后的寻找
// 不需要return,需要回溯尝试其他情况
count++;
} else {// 没有结束
// 深度优先递归
backtract(row+1);
}
// 回溯
removeQueen(row,col); // 移除皇后
}
}
}
public int totalNQueens(int n) {
this.n = n;
rows = new int[n];
hills = new int[4*n - 1];
dales = new int[2*n - 1];
queens = new int[n];
backtract(0);
return count;
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

