62、不同的路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。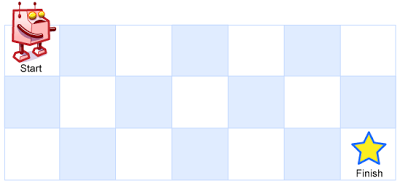
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28
题解
1 结合图形分析,寻求规律
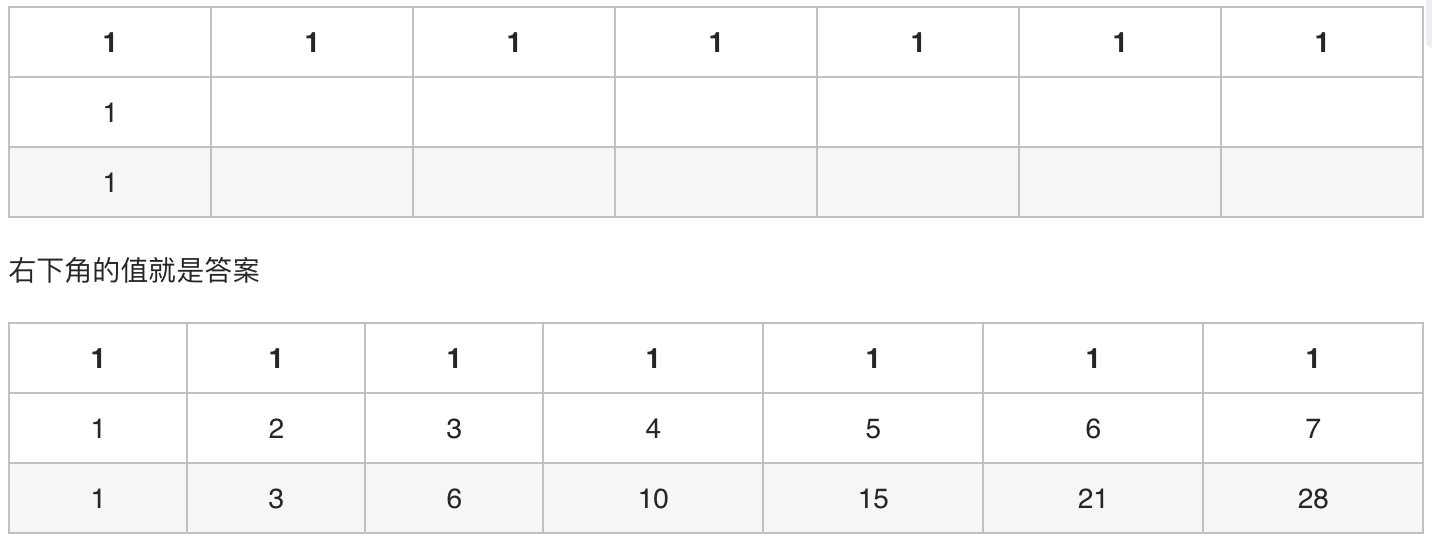
- 规律就是依次递增可以走的路径的个数
class Solution{
public int unquesPaths(int m,int n) {
int[] count = new int[n];
Arrays.fill(count,1);
for (int i = 1;i < m;i++) {
for (int j = 1;j < n;j++) {
count[j] += count[j - 1];
}
}
return count[n-1];
}
}
2、递归求解
- 深度优先搜索
未进行优化版
public int uniquePaths(int m,int n) {
return uniquePathsCore(1,1,m,n);
}
private int uniquePathsCore(int i,int j,int m,int n) {
if (i == m && j == n) {
return 1;
}
int c = 0,w = 0;
if (x < m) {
c = uniquePathsCore(i + 1,j,m,n);
}
if (y < n) {
w = uniquePathsCore(i,j + 1,m,n);
}
return c + w;
}
优化版
- 已经走过的路就标记一下
public int uniquePaths(int m,int n) {
HashMap<String,Integer> visited = new HashMap<>();
return uniquePathsCore(1,1,m,n,visited);
}
private int uniquePathsCore(int i,int j,int m,int n,HashMap<String,Integer> visited) {
if (i == m && j == n) {
return 1;
}
int c = 0,w = 0;
Srting key = i + 1 + "&" + j;
if (!visited.contain(key)){
if (i < m) {
c = uniquePathsCore(i + 1,j,m,n,visited);
}
} else { c = visited.get(key);}
key = i + "&" + (j+1);// java 编译器会优化字符串合并,j+1需要用()
if (!visited.contain(key)){
if (j < n) {
w = uniquePathsCore(i,j + 1,m,n,visied);
}
} else { w = visted.get(key);}
key = i + "&" + j;
visited.put(key,c+w);
return c + w;
}
3、动态规划
- 第一种方法就是
dp[i][j]记录到(i,j),所有可能的路径数量
public int uniquePaths(int m, int n) {
int[][] dp = new int[m+1][n+1];
dp[1][1] = 1;
for (int i = 1;i <= m;i++) {
for (int j = 1;j <= n;j++) {
if (i > 1 && j > 1) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
} else if (i == 1 && j > 1){
dp[i][j] = dp[i][j - 1];
} else if (i > 1 && j == 1) {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m][n];
}
数学分析
- 排列组合
- 分析
- 每种情况有必有
m-1步向右,n-1步向下,求这些的组合数即可。就是m-1个橘子,n-1个苹果的全排列。所有橘子都一样。所有苹果都一样。
- 每种情况有必有

public int uniquePaths(int m, int n) {
int N = n + m - 2;
int k = m - 1;
long res = 1;
for (int i = 1; i <= k; i++)
res = res * (N - k + i) / i;
return (int) res;
}
// 作者:windliang
// 链接:https://leetcode-cn.com/problems/unique-paths/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-20/
62、不同的路径II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
说明:m 和 n 的值均不超过 100。
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
题解
1、动态规划
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m+1][n+1];
dp[0][0] = 1;
for (int i = 0;i < m;i++) {
for (int j = 0;j < n;j++) {
if (obstacleGrid[i][j] != 1){// 没有障碍物
if (i > 0 && j > 0 ) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
} else if (i == 0 && j > 0){
dp[i][j] = dp[i][j - 1];
} else if (i > 0 && j == 0) {
dp[i][j] = dp[i - 1][j];
}
} else {
dp[i][j] = 0;// 障碍物处路径数为0
}
}
}
return dp[m-1][n-1];
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

