73、矩阵置零

leetcode 数组哈希表矩阵

Created At : 2020-07-26 00:19

Count:774 Views 👀 :

题目
分析

题目

给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。请使用原地算法。

示例 1:

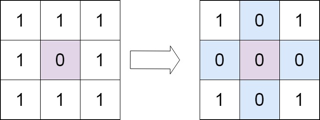
输入: 
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
输出: 
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

示例 2:

输入: 
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
输出: 
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]

进阶:

一个直接的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个常数空间的解决方案吗？

分析

原地算法的意思之使用原本的数组或者矩阵进行数据存储，保证时间复杂度 $S_n=O(1)$

空间复杂度为O(1)

以行首、列首进行标记，确定该行和该列是否应该为0

class Solution {
    public void setZeroes(int[][] matrix) {
        Boolean isCol = false;// 标记第一列是否要置零
        int R = matrix.length;
        int C = matrix[0].length;
        
        for (int i = 0;i < R; i++) {
            if (matrix[i][0] == 0) {
                isCol =  true;
            }
            // 标记需要置零的行和列
            for (int j = 1;j < C; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        // 由行列 来将交叉位置置零
        for (int i = 1; i < R;i++) {
            for (int j = 1;j < C;j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        // 第一行置零
        if (matrix[0][0] == 0){
            for (int j = 0;j < C;j++) {
                matrix[0][j] = 0;
            }
        }
        // 第一列置零
        if (isCol) {
            for (int i = 0;i < R;i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

如果`matrix[i][j]`等于0，将行列的值重置为特殊值，避免影响判断，然后再讲特殊值重置为0

暴力、空间复杂度为O(1)
原本等于零的值不动

class Solution {
  public void setZeroes(int[][] matrix) {
    int MODIFIED = -1000000;
    int R = matrix.length;
    int C = matrix[0].length;

    for (int r = 0; r < R; r++) {
      for (int c = 0; c < C; c++) {
        if (matrix[r][c] == 0) {
          for (int k = 0; k < C; k++) {
            if (matrix[r][k] != 0) {
              matrix[r][k] = MODIFIED;
            }
          }
          for (int k = 0; k < R; k++) {
            if (matrix[k][c] != 0) {
              matrix[k][c] = MODIFIED;
            }
          }
        }
      }
    }

    for (int r = 0; r < R; r++) {
      for (int c = 0; c < C; c++) {
        // Make a second pass and change all MODIFIED elements to 0 """
        if (matrix[r][c] == MODIFIED) {
          matrix[r][c] = 0;
        }
      }
    }
  }
}

// 链接：https://leetcode-cn.com/problems/set-matrix-zeroes/solution/ju-zhen-zhi-ling-by-leetcode/

存储要重置为0的行列下标，然后重置为0

空间复杂度为O(M+N)

class Solution{
    public void setZeroes(int[][] matrix) {
        int R = matrix.length;
        int C = matrix[0].length;

        Set<Integer> rows =  new HashSet<Integer>();
        Set<Integer> cols =  new HashSet<Integer>();

        for (int i = 0;i < R; i++) {
            for (int j = 0; j <C;j++) {
                if (matrix[i][j] == 0) {
                    rows.add(i);
                    cols.add(j);
                }
            }
        }

        for (int i = 0;i < R;i++) {
            for (int j = 0;j < C; j++) {
                if (rows.contains(i) || cols.contains(j)) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com