84、求最大的矩阵面积
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
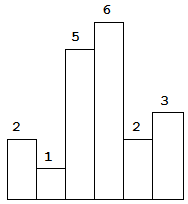
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
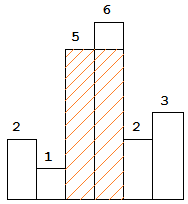
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
题解
1、暴力
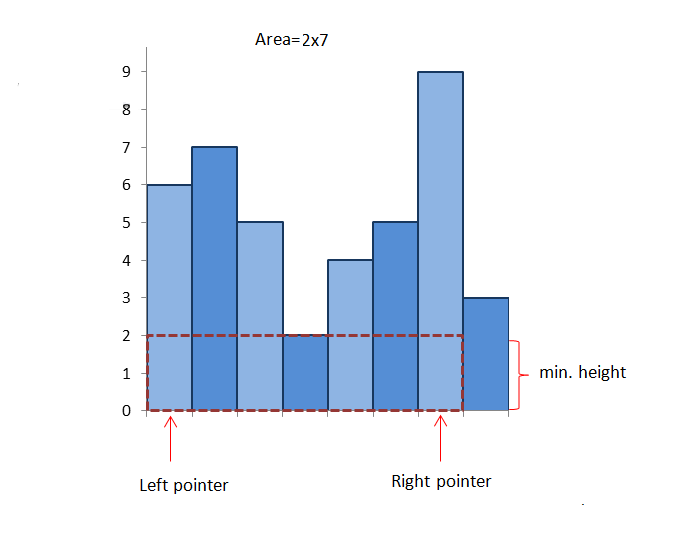
两个柱子间矩形的高由它们之间最矮的柱子决定,因此,我们可以考虑所有两两柱子之间形成的矩形面积,该矩形的高为它们之间最矮柱子的高度,宽为它们之间的距离,这样可以找到所要求的最大面积的矩形。
public class Solution {
public int largestRectangleArea(int[] heights) {
int maxarea = 0;
for (int i = 0; i < heights.length; i++) {
for (int j = i; j < heights.length; j++) {
int minheight = Integer.MAX_VALUE;
// 求[i,j]之间的最矮的高
for (int k = i; k <= j; k++) {
minheight = Math.min(minheight, heights[k]);
}
// 更新最大的面积
maxarea = Math.max(maxarea, minheight * (j - i + 1));
}
}
return maxarea;
}
}
2、暴力的优化
第一版的暴力重复比较了很多次,考虑用前一对柱子之间的最低高度来求出当前柱子对间的最低高度,来减少比较的次数。
用数学语言来表达
$minheight=\min(minheight, heights(j))$ ,其中, heights(j)是第 j 个柱子的高度
// 优化
public class Solution {
public int largestRectangleArea(int[] heights) {
int maxarea = 0;
for (int i = 0; i < heights.length; i++) {
int minheight = Integer.MAX_VALUE;// 记录从 i开始的最矮的矩形
for (int j = i; j < heights.length; j++) {
// 更新目前为止最矮的矩形
minheight = Math.min(minheight, heights[j]);
// 更新目前为止最大的矩形面积
// 新的值(minheight * (j - i + 1))与旧的值取大的一个
maxarea = Math.max(maxarea, minheight * (j - i + 1));
}
}
return maxarea;
}
}
// 链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode/
3、分治法
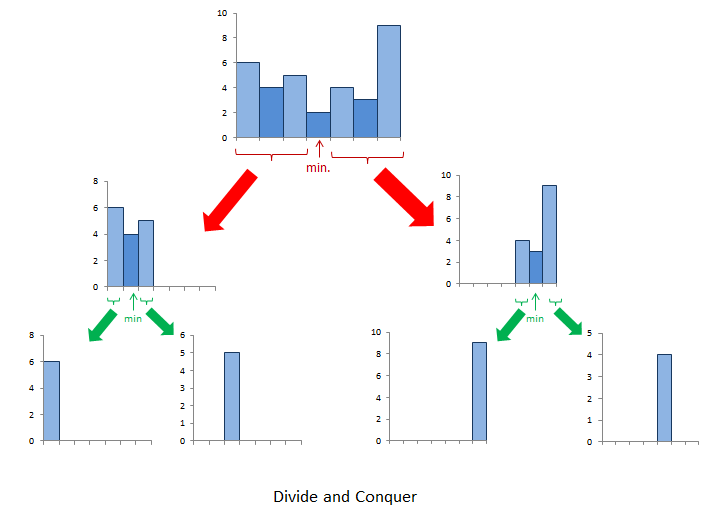
- 递归分治思想
- 按照最矮的柱子进行二分
- 最大矩形位于:
- 整个柱状图
- 最矮矩形的左边(子问题)
- 最矮矩形的右边(子问题)
public class Solution {
public int largestRectangleArea(int[] heights) {
return calculateArea(heights,0,heights.length - 1);
}
private int calculateArea(int[] heights,int start,int end){
// 递归结束判断
if (start > end) return 0;
// 求最矮矩形的下标
int minIndex = start;
for (int i = start;i <= end;i++){//耗时
if (heights[minIndex] > heights[i]){
minIndex = i;
}
}
// 二分递归
return Math.max(heights[minIndex]*(end - start + 1),Math.max(calculateArea(heights,start,minIndex - 1),calculateArea(heights,minIndex + 1,end)));
}
}
// 链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode/
4、利用栈
- 利用栈的特点,用栈存储当前遍历到的矩形的下标
public class Solution {
public int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<>();
stack.push(-1);
int maxarea = 0;
for (int i = 0;i < heights.length;i++) {
// 循环,直到遇到递增的矩形高度
while(stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
// 更新最大矩形的面积
maxarea = Math.max(maxarea,heights[stack.pop()]*(i - stack.peek() - 1));
}
// 矩形的下标入栈
stack.push(i);
}
while(stack.peek() != -1){
// 更新最大矩形的面结
maxarea = Math.max(maxarea,heights[stack.pop()]*(heights.length - stack.peek() - 1));
}
return maxarea;
}
}
// 链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode/
5、一来一回扫秒——单调栈
- 3min
class Solution {
public int largestRectangleArea(int[] heights) {
int n=heights.length;
if(n==0) return 0;
// 左侧最小矩形的下标存储
int []leftMin=new int[n];
// 右侧最小值下标存储
int []rightMin=new int[n];
leftMin[0]=-1;
rightMin[n-1]=n;
int res=0;
for(int i=1;i < n;i++)
{
int tmp=i-1;// i-1出的矩形最矮
// 递增就更新最矮矩形的下标tmp,否则不更新
while(tmp >= 0 && heights[tmp] >= heights[i])
{
tmp = leftMin[tmp];
}
// 第一个最矮的矩形的下标
leftMin[i] = tmp;// heights[i]的左侧扩展极限为tmp
}
for(int i=n-2;i >= 0;i--)
{
int tmp=i+1;
while(tmp<n && heights[tmp]>=heights[i])
{
tmp=rightMin[tmp];
}
rightMin[i]=tmp;// heights[i]的右侧扩展极限为tmp
}
// 利用leftmin 和 rightmin不断更新最大的矩形面积
for(int i = 0;i < n;i++)
{
// (rightMin[i]-leftMin[i]-1 矩形长度
res=Math.max(res,(rightMin[i]-leftMin[i]-1)*heights[i]);
}
return res;
}
}
6、混合解法:排序数组判断,递归更新最大值
- 1ms 递归
class Solution {
public int largestRectangleArea(int[] heights) {
return helper(heights, 0, heights.length - 1);
}
private int helper(int[] heights, int start, int end){
if(start > end){
return 0;
}
if(start == end){
return heights[start];
}
int min = heights[start];
boolean sorted = true;
for(int i = start + 1; i <= end; i++){// 求当前区间的最小值。 判断是否是非递减的
// 更新最矮矩形的高度
min = Math.min(min, heights[i]);
if(heights[i - 1] > heights[i]){
sorted = false;
}
}
if(sorted){// 排好序的直接遍历一遍求最大值
int max = 0;
for(int i = start; i <= end; i++){
max = Math.max(max, heights[i] * (end - i + 1));
}
return max;
}
int area = min * (end - start + 1);
int startIndex = start;
for(int i = start; i <= end; i++){
if(heights[i] == min){// 当前位置是最小值
area = Math.max(area, helper(heights, startIndex, i - 1));// 递归
startIndex = i + 1;
}
}
return Math.max(area, helper(heights, startIndex, end));// 递归
}
}
``
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

