892、三维形体的表面积

leetcode

Created At : 2020-07-26 00:19

Count:469 Views 👀 :

Comment:

892、三维形体是的表面积
题解
1. 1、分步累加

892、三维形体是的表面积

在 N * N 的网格上，我们放置一些 1 * 1 * 1 的立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。

请你返回最终形体的表面积。

示例 1：

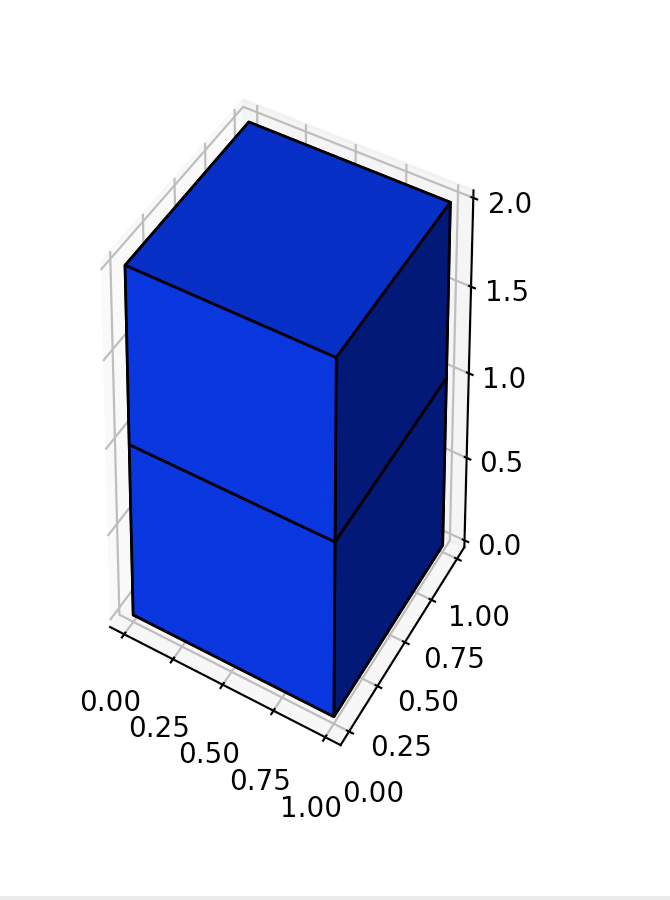
输入：[[2]]
输出：10

示例 2：

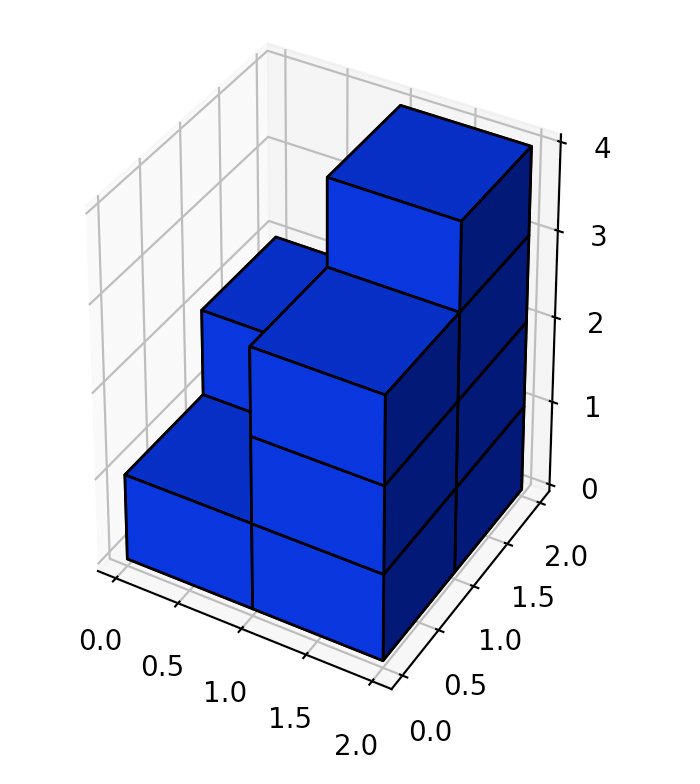
输入：[[1,2],[3,4]]
输出：34

示例 3：

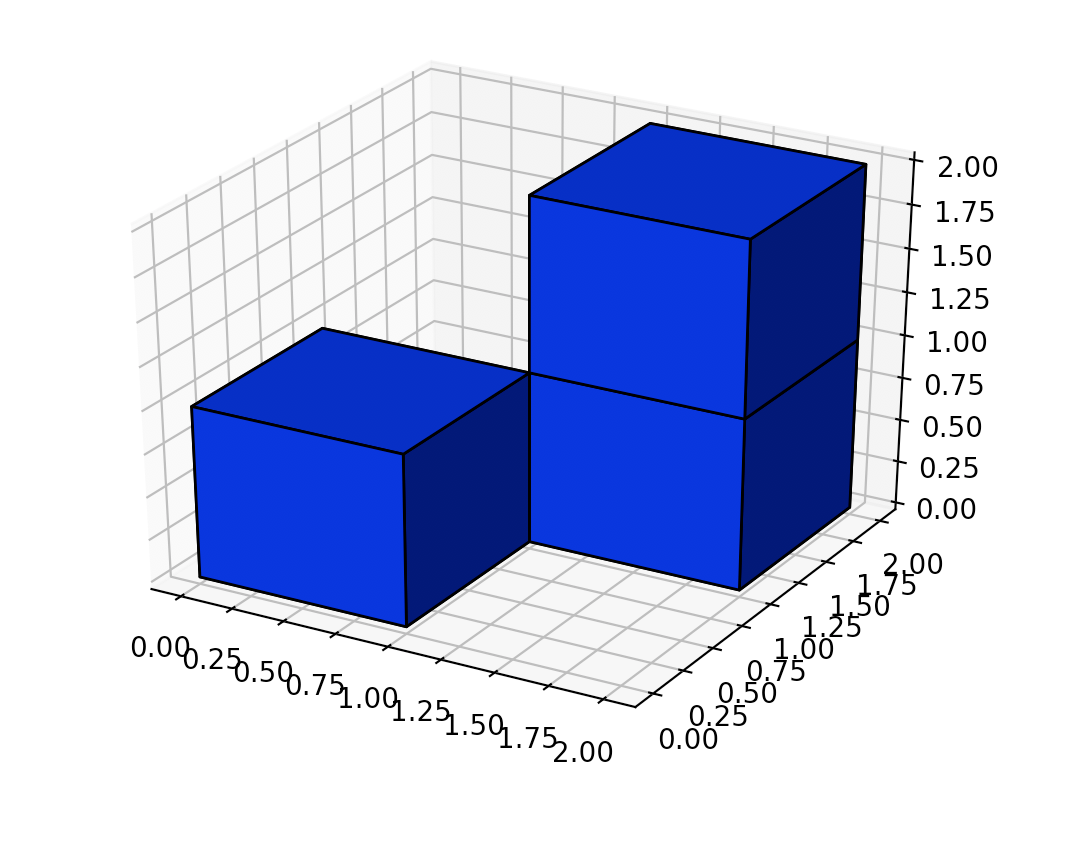
输入：[[1,0],[0,2]]
输出：16

示例 4：

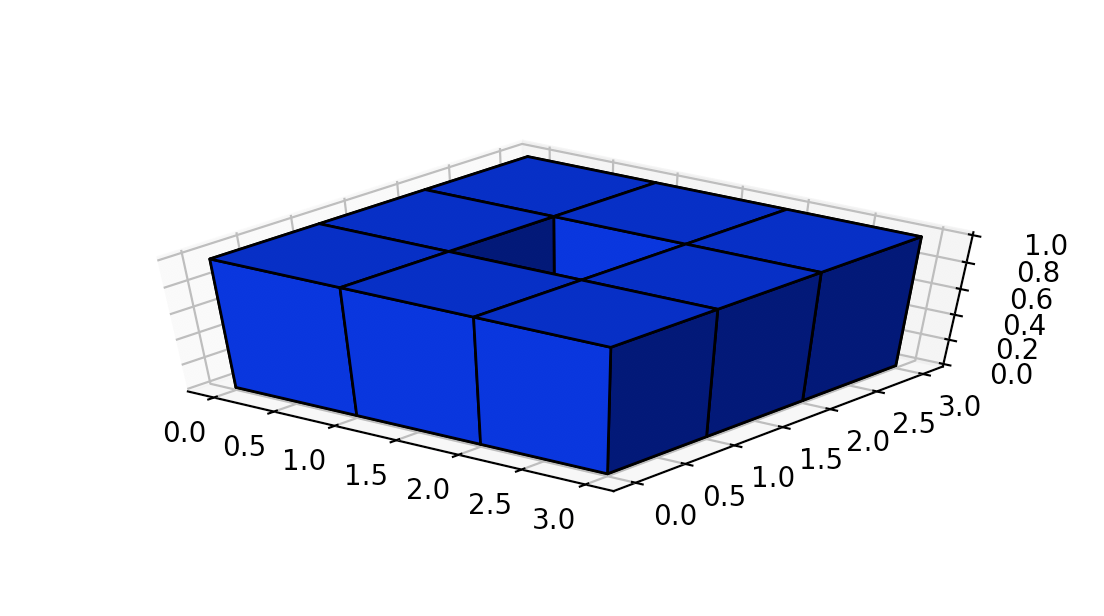
输入：[[1,1,1],[1,0,1],[1,1,1]]
输出：32

示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]]
输出：46

提示：

1 <= N <= 50
0 <= grid[i][j] <= 50

链接：https://leetcode-cn.com/problems/surface-area-of-3d-shapes

题解

正方形网格，上有干个堆叠的立方体。

1、分步累加

遍历所有网格。

class Solution {
    public int surfaceArea(int[][] grid) {
        // 方向控制
        int[] dr = new int[]{0,0,1,-1};
        int[] dc = new int[]{1,-1,0,0};

        int N = grid.length;
        int ans  = 0;

        // 遍历所有网格
        for (int i = 0;i < N;i++) {
            for (int j = 0;j < N;j++) {
                if (grid[i][j] > 0) {
                    // 上面和底面
                    ans+=2;
                    // 抵消的侧面积
                    int side = 0;
                    for (int k = 0;k < 4;k++) {
                        int nr = i + dr[k];
                        int nc = j + dc[k];
                        if (nr >= 0 && nr < N && nc >= 0 && nc < N) {
                            side += Math.min(grid[nr][nc],grid[i][j]);
                        }
                    }
                    // 侧面
                    ans += grid[i][j]*4-side;
                }
            }
        }
        return ans;
    }
}

按照方向极端抵消面积

class Solution {
    public int surfaceArea(int[][] grid) {
        int surface = 0;
        int n = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                n = grid[i][j];
                if (n > 0) {
                    // 计算出来无侧面抵消的表面积，2 * (n - 1)是上下抵消
                    surface += 6 * n - 2 * (n - 1);
                    // 左侧面抵消
                    if (i > 0) {
                        surface -= 2 * Math.min(n, grid[i-1][j]);
                    }
                    // 右侧面抵消
                    if (j > 0) {
                        surface -= 2 * Math.min(n, grid[i][j-1]);
                    }        
                }
            }
        }
        return surface;
    }
}

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com