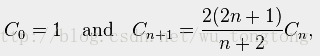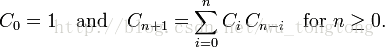95、不同的二叉搜索树II
给定一个整数 n,生成所有由 1 … n 为节点所组成的二叉搜索树。
示例:
输入: 3
输出:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
解释:
- 以上的输出对应以下 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
背景
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为(从第零项开始) :
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
卡特兰数Cn满足以下递推关系:
思路
我们从序列 1 ..n 中取出数字 i,作为当前树的树根。于是,剩余 i - 1 个元素可用于左子树,n - i 个元素用于右子树。
如 前文所述,这样会产生 G(i - 1) 种左子树 和 G(n - i) 种右子树,其中 G 是卡特兰数。
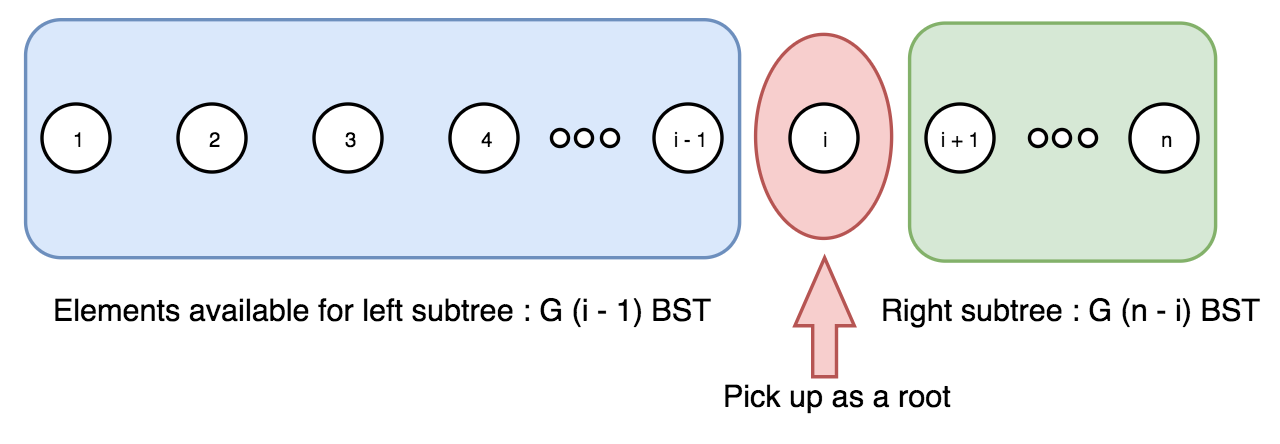
现在,我们对序列 1 … i - 1 重复上述过程,以构建所有的左子树;然后对 i + 1 … n 重复,以构建所有的右子树。
这样,我们就有了树根 i 和可能的左子树、右子树的列表。
最后一步,对两个列表循环,将左子树和右子树连接在根上。
代码
- 递归,
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<TreeNode> generateTrees(int n) {
if (n == 0) {
return new LinkedList<TreeNode>();
}
return getTreesCore(1,n);
}
private LinkedList<TreeNode> getTreesCore(int start,int end) {
LinkedList<TreeNode> all = new LinkedList<>();
// 退出递归
if (start>end) {
all.add(null);
return all;
}
// 全局递归二分
for (int i = start;i <= end;i++) {
// 递归左半部分
LinkedList<TreeNode> left = getTreesCore(start,i-1);
// 递归右半部分
LinkedList<TreeNode> right = getTreesCore(i+1,end);
for (TreeNode l : left) {
for (TreeNode r:right) {
TreeNode node = new TreeNode(i);
node.left = l;
node.right = r;
all.add(node);
}
}
}
return all;
}
}
- 动态规划
- dp[i]表示,0-i中的搜索二叉树的类别
public List<TreeNode> generateTrees(int n) {
ArrayList<TreeNode>[] dp = new ArrayList[n + 1];
dp[0] = new ArrayList<TreeNode>();
if (n == 0) {
return dp[0];
}
dp[0].add(null);
for (int len = 1;len <= n; len++) {
dp[len] = new ArrayList<TreeNode>();
for (int root = 1;root <= len;root++) {
int left = root - 1;
int right = len - root;
for (TreeNode l : dp[left]) {
for (TreeNode r: dp[right]) {
TreeNode node = new TreeNode(root);
node.left = l;
node.right = clone(r,root);
dp[len].add(node);
}
}
}
}
return dp[n];
}
private TreeNode clone(TreeNode n,int offset) {
if (n == null) {
return null;
}
// 深复制
TreeNode node = new TreeNode(n.val + offset);
// 递归复制
node.left = clone(n.left,offset);
node.right = clone(n.right,offset);
return node;
}
- 动态规划优化,由已知的解更新未知的解
public List<TreeNode> generateTrees(int n) {
List<TreeNode> pre = new ArrayList<TreeNode>();
if (n == 0) {
return pre;
}
pre.add(null);
// 每次增加一个数字 dp[i]
for (int i = 1; i <= n; i++) {
List<TreeNode> cur = new ArrayList<TreeNode>();
// 遍历之前的所有解
for (TreeNode root : pre) {
//插入到根节点
TreeNode insert = new TreeNode(i);
insert.left = root;
cur.add(insert);
//插入到右孩子,右孩子的右孩子...最多找 n 次孩子
for (int j = 0; j <= n; j++) {
TreeNode root_copy = treeCopy(root); //复制当前的树
TreeNode right = root_copy; //找到要插入右孩子的位置
int k = 0;
//遍历 j 次找最右孩子
for (; k < j; k++) {
if (right == null)
break;
right = right.right;
}
//到达 null 提前结束
if (right == null)
break;
//保存当前右孩子的位置的子树作为插入节点的左孩子
TreeNode rightTree = right.right;
insert = new TreeNode(i);
right.right = insert; //右孩子是插入的节点
insert.left = rightTree; //插入节点的左孩子更新为插入位置之前的子树
//加入结果中
cur.add(root_copy);
}
}
pre = cur;
}
return pre;
}
private TreeNode treeCopy(TreeNode root) {
if (root == null) {
return root;
}
TreeNode newRoot = new TreeNode(root.val);
newRoot.left = treeCopy(root.left);
newRoot.right = treeCopy(root.right);
return newRoot;
}
// 作者:windliang
// 链接:https://leetcode-cn.com/problems/unique-binary-search-trees-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-2-7/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
96、不同的二叉搜索树
给定一个整数 n,求以 1 … n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
思路
这种的二叉树满足卡特兰树数组,
1. 动态规划
G(n)表示节点数为n的不同二叉搜索树的个数F(i,n)表示以i为根的不同二叉树的个数(1<= i <= n)
$$
G(i) = \sum_{i=1}^n F(i,n)
$$F(i,n)与G(i-1)和G(n-i)的关系是:
$$
F(i,n) = G(i-1)·G(n-i)
$$
所以,
$$
G(i) = \sum_{i=1}^n G(i-1)·G(n-i)
$$
2. 数学演绎
- 卡特兰数
$$
C_0 = 1, C_{n+1} = \frac{2(2n+1)}{n+2}C_n
$$
代码
- 动态规划
public class Solution{
public int numTrees(int n) {
int[] G = new int[n+1];
G[0] = G[1] = 1;
for (int i = 2;i <= n;i++) {
for (int j = 1;j <= i;j++) {
G[i] += G[j-1]*G[i-j];
}
}
return G[n];
}
}
- 数学演绎法
public class Solution{
public int numTrees(int n) {
long C = 1;// 可能会超过int
for (int i = 1;i < n;i++) {
C = C*2*i*(2*i+1)/(i+2);
}
return (int)C;
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com