LCP4、覆盖
你有一块棋盘,棋盘上有一些格子已经坏掉了。你还有无穷块大小为1 * 2的多米诺骨牌,你想把这些骨牌不重叠地覆盖在完好的格子上,请找出你最多能在棋盘上放多少块骨牌?这些骨牌可以横着或者竖着放。
输入:n, m代表棋盘的大小;broken是一个b * 2的二维数组,其中每个元素代表棋盘上每一个坏掉的格子的位置。
输出:一个整数,代表最多能在棋盘上放的骨牌数。
示例 1:
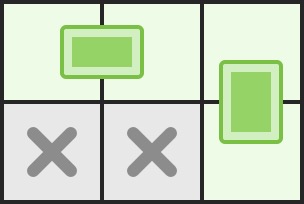
输入:n = 2, m = 3, broken = [[1, 0], [1, 1]]
输出:2
解释:我们最多可以放两块骨牌:[[0, 0], [0, 1]]以及[[0, 2], [1, 2]]。(见下图)
示例 2:
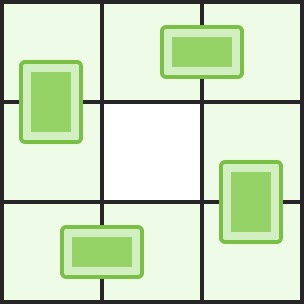
输入:n = 3, m = 3, broken = []
输出:4
解释:下图是其中一种可行的摆放方式
限制:
1 <= n <= 8
1 <= m <= 8
0 <= b <= n * m
代码
// mat二分匹配图 from起始点
int mat[105][105], from[105], nn, mm;
bool vis[105];// 访问记录
bool unvisible[10][10];// 不可到达的地点
int match(int x){
for (int i = 0; i < nn * mm; ++i){
int dx = i / mm, dy = i % mm;
if ((dx + dy) & 1) continue;// 黑色位置,跳过
if (unvisible[dx][dy]) continue;// 不可到达
if (!mat[x][i]) continue;// 已匹配
if (!vis[i]){// 未访问
vis[i] = true;
if (from[i] < 0 || match(from[i])){// 递归匹配
from[i] = x;
return 1;
}
}
}
return 0;
}
int Hungary(){
// 认为 (x 坐标 + y 坐标) 为奇数时格子是黑色,对黑色格子找匹配
int match_size = 0;
memset(from, -1, sizeof(from));
for (int i = 0; i < nn * mm; ++i){
int dx = i / mm, dy = i % mm;
if (!((dx + dy) & 1)) continue;// 白色跳过
if (unvisible[dx][dy]) continue;// 不可到达跳过
memset(vis, 0, sizeof(vis));// 重置访问集合
match_size += match(i);// 统计匹配集大大小
}
return match_size;
}
class Solution {
public:
int domino(int n, int m, vector<vector<int>>& broken) {
nn = n, mm = m;
memset(unvisible, 0, sizeof(unvisible));
// 初始化不可到达位置
for (vector<int>& p: broken)
unvisible[p[0]][p[1]] = true;
// 初始化邻接矩阵
memset(mat, 0, sizeof(mat));
// 初始化匹配
for (int i = 0; i < n; ++i){
for (int j = 0; j < m; ++j){
if (unvisible[i][j]) continue;
int id = i * m + j; // 将节点按照 (x 坐标 * m) + (y 坐标) 编号
// 右边的格子
if (j + 1 < m && unvisible[i][j + 1] == false){
int iid = i * m + j + 1;
mat[id][iid] = mat[iid][id] = 1;// 连接两个位置
}
// 下面的格子
if (i + 1 < n && unvisible[i + 1][j] == false){
int iid = (i + 1) * m + j;
mat[id][iid] = mat[iid][id] = 1;// 连接两个位置
}
}
}
return Hungary();
}
};
// 作者:zqy1018
// 链接:https://leetcode-cn.com/problems/broken-board-dominoes/solution/c-er-fen-tu-zui-da-pi-pei-by-zqy1018/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

