使用 oh-my-zsh

题目

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

示例:

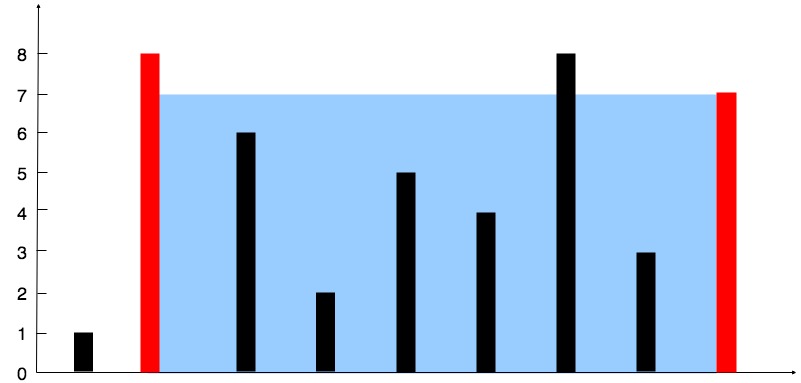
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

• 提示：
  • $n == height.length$
  • $2 <= n <= 10^5$
  • $0 <= height[i] <= 10^4$

分析

暴力思路：穷举，求面积，返回最大的面积。
双指针：谁小，谁移动，计算面积，返回最大值

1、双指针法

• 左右指针，对应位置的数值，小的指针移动
  • a[l] < a[r] l++
  • a[l] >= a[r] r–

class Solution {
    public int maxArea(int[] height) {
        int l = 0,r = height.length - 1;
        int maxArea = 0;

        while (l < r) {
            // 计算并更新最大面积
            maxArea = Math.max(Math.min(height[l],height[r]) * (r - l), maxArea);
 
            // 左侧短板
            if (height[l] < height[r]) {
                l++;
            } else { // 右侧短板
                r--;
            }
        }

        return maxArea;
    }
}

// 连续较小值，优化，减少数学运算的次数

class Solution {
    public int maxArea(int[] height) {
        int res = 0;
        int left = 0, right = height.length-1;
        while (left < right) {
            res = Math.max((right-left) * Math.min(height[left],height[right]), res);
            if (height[right] > height[left]) {
                int cur = height[left];
                // 优化左侧 重复高度值或者小于的高度
                while (left < right && height[left] <= cur) {
                    left ++;
                }
            }
            else {
                int cur = height[right];
                // 优化右侧 重复高度值或者小于的高度
                while (left < right && height[right] <= cur) {
                    right --;
                }
            }
        }
        return res;
    }
}

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com