使用 oh-my-zsh

有一些不规则的硬币。在这些硬币中，prob[i] 表示第 i 枚硬币正面朝上的概率。

请对每一枚硬币抛掷 一次，然后返回正面朝上的硬币数等于 target 的概率。

示例 1：

输入：prob = [0.4], target = 1
输出：0.40000

示例 2：

输入：prob = [0.5,0.5,0.5,0.5,0.5], target = 0
输出：0.03125

提示：

• 1 <= prob.length <= 1000
• 0 <= prob[i] <= 1
• 0 <= target <= prob.length
• 如果答案与标准答案的误差在 $10^{-5}$ 内，则被视为正确答案。

分析

1、递归动态规划 $O(ntarget) O(ntarget)$

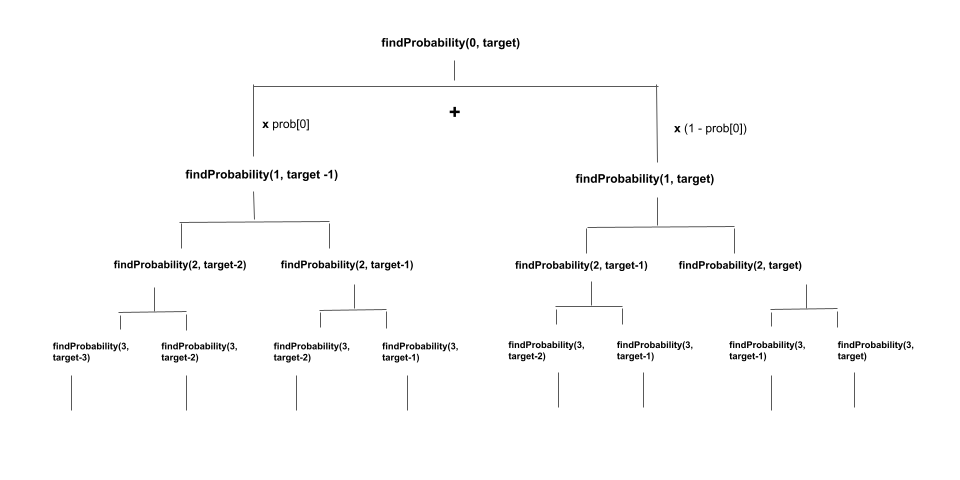
需要记忆化数组，进行剪枝。

class Solution {
    private double findProbability(int index, int n, double[][] memo, double[] prob, int target) {
        // 如果 target 小于 0，则返回 0，因为我们有比需要的更多的正面
        if (target < 0) {
            return 0;
        }
        // 扔完所有的硬币后，如果我们得到了所需的正面数，
        // 返回 1 来计数这个情况，否则返回 0。
        if (index == n) {
            return target == 0 ? 1 : 0;
        }

        if (memo[index][target] != -1) {
            return memo[index][target];
        }

        // index target处的概率等于下一次抛硬币的相反情况各自概率的相加
        memo[index][target] = findProbability(index + 1, n, memo, prob, target - 1) * prob[index] + findProbability(index + 1, n, memo, prob, target) * (1 - prob[index]);

        return memo[index][target];
    }

    public double probabilityOfHeads(double[] prob, int target) {
        int n = prob.length;
        double[][] memo = new double[n][target + 1];
        for (double[] row : memo) {
            Arrays.fill(row, -1);
        }

        return findProbability(0, n, memo, prob, target);
    }
}

2、迭代动态规划 $O(ntarget) O(ntarget)$

递归 写法转 动态规划。

使用一个二维数组 dp，其中 dp[i][j] 表示使用前 i 个硬币获得 j 个正面的概率。 dp[n][target] 是我们的答案，其中 n 是硬币的总数。

class Solution {
    public double probabilityOfHeads(double[] prob, int target) {
        int n = prob.length;
        double[][] dp = new double[n + 1][target + 1];
        dp[0][0] = 1;

        for (int i = 1; i <= n; i++) {
            dp[i][0] = dp[i - 1][0] * (1 - prob[i - 1]);
            for (int j = 1; j <= target && j <= i; j++) {
                dp[i][j] = dp[i - 1][j - 1] * prob[i - 1] + dp[i - 1][j] * (1 - prob[i - 1]);
            }
        }

        return dp[n][target];
    }
}

3、空间优化的动态规划 $O(n*target) O(target)$

dp数组复用，减少空间复杂度。

class Solution {
    public double probabilityOfHeads(double[] prob, int target) {
        int n = prob.length;
        double[] dp = new double[target + 1];
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
            for (int j = target; j >= 1; j--) {
                dp[j] = dp[j - 1] * prob[i - 1] + dp[j] * (1 - prob[i - 1]);
            }
            dp[0] = dp[0] * (1 - prob[i - 1]);// 更新dp[0]
        }

        return dp[target];
    }
}

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com