题目
给你一棵无根带权树,树中总共有 n 个节点,分别表示 n 个服务器,服务器从 0 到 n - 1 编号。同时给你一个数组 edges ,其中 edges[i] = [ai, bi, weighti] 表示节点 $a_i$ 和 $b_i$ 之间有一条双向边,边的权值为 $weight_i$ 。再给你一个整数 signalSpeed 。
如果两个服务器 a ,b 和 c 满足以下条件,那么我们称服务器 a 和 b 是通过服务器 c 可连接的 :
a < b,a != c且b != c。- 从 c 到 a 的距离是可以被
signalSpeed整除的。 - 从 c 到 b 的距离是可以被
signalSpeed整除的。 - 从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。
请你返回一个长度为 n 的整数数组 count ,其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。
示例 1:
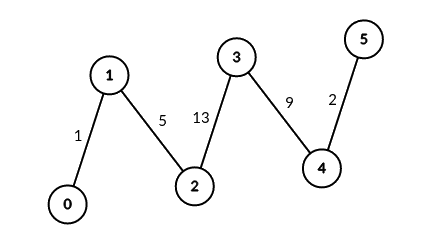
输入:edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
输出:[0,4,6,6,4,0]
解释:由于 signalSpeed 等于 1 ,count[c] 等于所有从 c 开始且没有公共边的路径对数目。
- 节点0:只有一个直接相连的节点,所以他没有中继节点的能力
- 节点1:存在的可连接(a,b) 有:(0,2) (0,3) (0,4) (0,5)
- 节点2:存在的可连接(a,b) 有: (0,3) (0,4) (0,5) (1,3) (1,4) (1,5)
- 节点3:存在的可连接(a,b) 有:(1,4) (1,5) (0,4) (0,5) (2,4) (2,5)
- 节点4:存在的可连接(a,b) 有:(0,5) (1,5) (2,5) (3,5)
- 节点5:只有一个直接相连的节点,所以他没有中继节点的能力
示例 2:
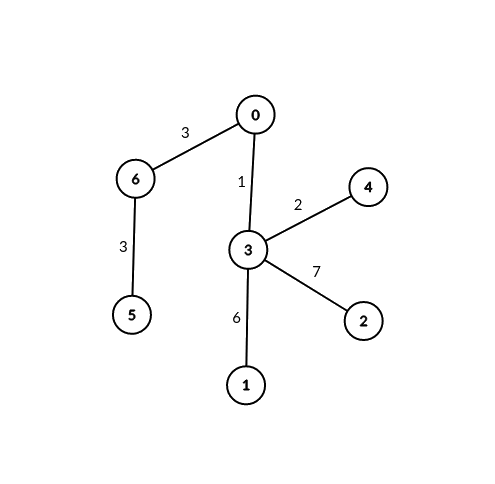
输入:edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
输出:[2,0,0,0,0,0,2]
解释:通过服务器 0 ,有 2 个可连接服务器对(4, 5) 和 (4, 6) 。
通过服务器 6 ,有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。
所有服务器对都必须通过服务器 0 或 6 才可连接,所以其他服务器对应的可连接服务器对数目都为 0 。
提示:
2 <= n <= 1000edges.length == n - 1edges[i].length == 30 <=$a_i$, $b_i$< nedges[i] = [$a_i$, $b_i$, $weight_i$]- $1 <= weighti <= 10^6$
- $1 <= signalSpeed <= 10^6$
- 输入保证 edges 构成一棵合法的树。
分析
题目中给了每个边的数据,包括:两个节点和权值。我们需要转换成邻接表,方便写深度优先搜索算法。
由于是无向边,通过边,我们可以扩展邻接表,把间接相连的节点,通过合并边的权值进行合并。
根据c可连接a,b的条件,可以再深度优先搜索中,进行计算,判断当前a,b是否可以连接。
构造邻接表 + 深度优先搜索
class Solution {
public int[] countPairsOfConnectableServers(int[][] edges, int signalSpeed) {
int n = edges.length + 1;
List<int[]>[] g = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
// 构造每个节点的邻接链表
for (int[] e : edges) {
int x = e[0];
int y = e[1];
int wt = e[2];
g[x].add(new int[]{y, wt});
g[y].add(new int[]{x, wt});
}
int[] ans = new int[n];
for (int i = 0;i < n;i++) { // 对于每个节点
int sum = 0;
for (int[] e : g[i]) {// 深度优先搜索邻接链表
int cnt = dfs(e[0], i, e[1], g, signalSpeed);
ans[i] += cnt * sum;
sum += cnt;
}
}
return ans;
}
private int dfs(int x, int fa, int sum, List<int[]>[] g, int signalSpeed) {
int cnt = sum % signalSpeed == 0? 1:0;// 当前x节点是否可以连接
// x 的邻接表
for (int[] e: g[x]) {
int y = e[0];
if (y != fa) { // 避免返回了,即单向递归搜索
// 递归,更新权值
cnt += dfs(y,x, sum + e[1], g, signalSpeed);
}
}
return cnt;
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

