给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat,你可以选择任一单元格作为 起始单元格 。
从起始单元格出发,你可以移动到 同一行或同一列 中的任何其他单元格,但前提是目标单元格的值 严格大于 当前单元格的值。
你可以多次重复这一过程,从一个单元格移动到另一个单元格,直到无法再进行任何移动。
请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。
返回一个表示可访问单元格最大数量的整数。
示例 1:
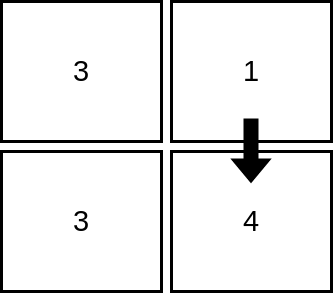
输入:mat = [[3,1],[3,4]]
输出:2
解释:上图展示了从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 2 个单元格,因此答案是 2 。
示例 2:
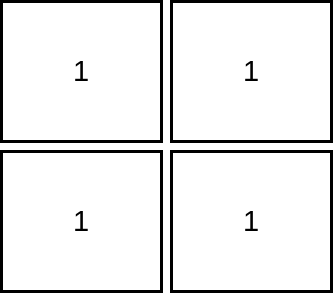
输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,在本示例中只能访问 1 个单元格。
示例 3:
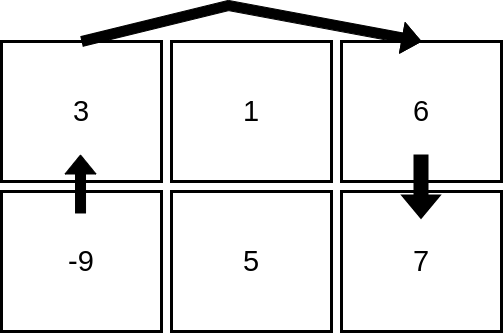
输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:上图展示了从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。可以证明,无论从哪个单元格开始,最多只能访问 4 个单元格,因此答案是 4 。
提示:
m == mat.lengthn == mat[i].length- $1 <= m, n <= 10^5$
- $1 <= m * n <= 10^5$
- $-10^5 <= mat[i][j] <= 10^5$
分析
按照严格递增实施矩阵搜索。
深度优先搜索
- 递归,入参:矩阵、当前位置、访问矩阵,长度
- 每次在行列上搜索最小的较大值,长度
- 访问标记 & 回溯处理
- 每一行每一列的排序和下标索引
无法通过Case:
mat =
[[7,6,3],
[-7,-5,6],
[-7,0,-4],
[6,6,0],
[-8,6,0]]
输出:6
预期输出:7
class Solution {
int m;
int n;
public int maxIncreasingCells(int[][] mat) {
// 明显的深度优先搜索
// 递归,每次在行列上搜索最小的较大值
m = mat.length;
n = mat[0].length;
int[][] visited = new int[m][n];
int ans = 0;
// 从最小的入手
for (int i = 0;i < m;i++) {
int minIndex = 0;
int minValue = 10001;
// 遍历每一列最小值
for (int j = 0;j < n;j++) {
if (minValue > mat[i][j]) {
minIndex = j;
minValue = mat[i][j];
}
}
visited[i][minIndex] = 1;// 标记最小值
ans = Math.max(ans, dfs(mat,i,minIndex,visited, 1));// 开始查找最长的递增序列
visited[i][minIndex] = 0;
}
// 从最小的入手
for (int i = 0;i < n;i++) {
int minIndex = 0;
int minValue = 10001;
// 遍历每一列最小值
for (int j = 0;j < m;j++) {
if (minValue > mat[j][i]) {
minIndex = j;
minValue = mat[j][i];
}
}
visited[minIndex][i] = 1;// 标记最小值
ans = Math.max(ans, dfs(mat,minIndex,i,visited, 1));// 开始查找最长的递增序列
visited[minIndex][i] = 0;
}
return ans;
}
public int dfs(int[][] mat, int k,int t,int[][] visited,int ans) {
int minValue = mat[k][t];
int minValue1 = 10001;
int minIndex = 0;
for (int i = 0;i < m;i++) {
if (visited[i][t] == 0) {
if (minValue < mat[i][t] && mat[i][t] < minValue1) {
minValue1 = mat[i][t];
minIndex = i;
}
}
}
int ans1 = ans;
if (minValue1 != 10001) {
visited[minIndex][t] = 1;
ans1 = dfs(mat, minIndex,t,visited,ans + 1);
visited[minIndex][t] = 0;
}
minValue1 = 10001;
for (int j = 0;j < n;j++) {
if (visited[k][j] == 0) {
if (minValue < mat[k][j] && mat[k][j] < minValue1) {
minValue1 = mat[k][j];
minIndex = j;
}
}
}
int ans2 = ans;
if (minValue1 != 10001) {
visited[k][minIndex] = 1;
ans2 = dfs(mat, k, minIndex,visited, ans + 1);
visited[k][minIndex] = 0;
}
return Math.max(ans1, ans2);
}
}
动态规划
$ T = O(mnlog(mn)) \ S = O(mn)$
- 初始化 行、列数量
- 初始化TreeMap
- 构建值下标映射,按照值从小到大有序
- 初始化最长长度ans,初始化行列最值数组
- 从小到大遍历值的下标数组
- 初始化极值数组
- 遍历所有位置
- 求出行、列最大值,更新fs,更新ans
- 遍历所有位置
- 更新行列最大值
- 返回结果ans
class Solution {
public int maxIncreasingCells(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
// 构建value下标映射,有序
TreeMap<Integer,List<int[]>> g = new TreeMap<>();
for (int i = 0;i < m;i++) {
for (int j = 0;j < n;j++) {
// 统计值- 位置的索引树
g.computeIfAbsent(mat[i][j], k -> new ArrayList<>()).add(new int[]{i , j});
}
}
int ans = 0;
int[] rowMax = new int[m];
int[] colMax = new int[n];
// 从小到大遍历每个key的所有的位置
for (List<int[]> pos : g.values()) {
int[] fs = new int[pos.size()];// 极值数组
// 遍历所有位置,求出行、列最大值,更新fs,更新ans
for (int k = 0;k < pos.size();k++) {
int[] p = pos.get(k);
int i = p[0];
int j = p[1];
fs[k] = Math.max(rowMax[i], colMax[j]) + 1;
ans = Math.max(ans, fs[k]);
}
// 遍历所有位置, 更新行列最大值
for (int k = 0;k < pos.size();k++) {
int[] p = pos.get(k);
int i = p[0];
int j = p[1];
// 更新i行最大值
rowMax[i] = Math.max(rowMax[i], fs[k]);
// 更新j列最大值
colMax[j] = Math.max(colMax[j], fs[k]);
}
}
return ans;
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

