题目
给你一张 无向 图,图中有 n 个节点,节点编号从 0 到 n - 1 (都包括)。同时给你一个下标从 0 开始的整数数组 values ,其中 values[i] 是第 i 个节点的 价值 。同时给你一个下标从 0 开始的二维整数数组 edges ,其中 edges[j] = [uj, vj, timej] 表示节点 uj 和 vj 之间有一条需要 timej 秒才能通过的无向边。最后,给你一个整数 maxTime 。
合法路径 指的是图中任意一条从节点 0 开始,最终回到节点 0 ,且花费的总时间 不超过 maxTime 秒的一条路径。你可以访问一个节点任意次。一条合法路径的 价值 定义为路径中 不同节点 的价值 之和 (每个节点的价值 至多 算入价值总和中一次)。
请你返回一条合法路径的 最大 价值。
注意:每个节点 至多 有 四条 边与之相连。
示例 1:
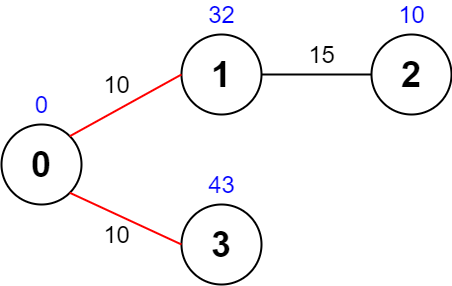
输入:values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
输出:75
解释:
一条可能的路径为:0 -> 1 -> 0 -> 3 -> 0 。总花费时间为 10 + 10 + 10 + 10 = 40 <= 49 。
访问过的节点为 0 ,1 和 3 ,最大路径价值为 0 + 32 + 43 = 75 。
示例 2:
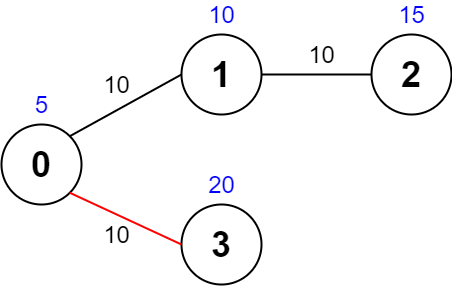
输入:values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
输出:25
解释:
一条可能的路径为:0 -> 3 -> 0 。总花费时间为 10 + 10 = 20 <= 30 。
访问过的节点为 0 和 3 ,最大路径价值为 5 + 20 = 25 。
示例 3:
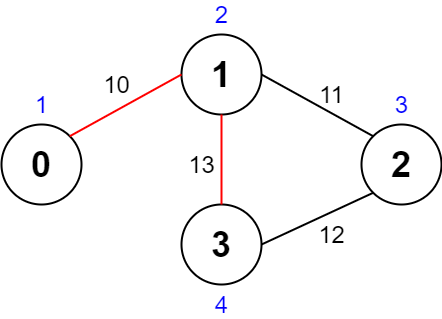
输入:values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
输出:7
解释:
一条可能的路径为:0 -> 1 -> 3 -> 1 -> 0 。总花费时间为 10 + 13 + 13 + 10 = 46 <= 50 。
访问过的节点为 0 ,1 和 3 ,最大路径价值为 1 + 2 + 4 = 7 。
示例 4:
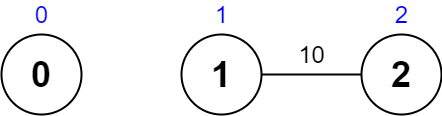
输入:values = [0,1,2], edges = [[1,2,10]], maxTime = 10
输出:0
解释:
唯一一条路径为 0 。总花费时间为 0 。
唯一访问过的节点为 0 ,最大路径价值为 0 。
提示:
n == values.length1 <= n <= 1000- $0 <= values[i] <= 10^8$
0 <= edges.length <= 2000edges[j].length == 30 <= uj < vj <= n - 110 <= timej, maxTime <= 100[uj, vj]所有节点对 互不相同 。- 每个节点 至多有四条 边。
- 图可能不连通。
分析
从无向图中,用最小的时间,从节点0开始遍历足够多的节点,获取最大的价值。
尽可能的走更多的价值高的节点。
- 存在环,按照环的顺序,尽可能的减少重复路程
- 时间足够的情况下,可以在环中节点按照非环的顺序遍历
- 时间不足够走完最简单的环的时候,需要选择性折返
- 不存在,必定存在重复路程
- 只有0节点存在的连通域,才能进行遍历取值
深度优先搜索
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

