3112、访问消失节点的最小时间

题目

一个公司在全国有 n 个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。

两个分部之间的 距离 是通过道路长度之和的 最小值 。

给你整数 n ，maxDistance 和下标从 0 开始的二维整数数组 roads ，其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过 maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

示例 1：

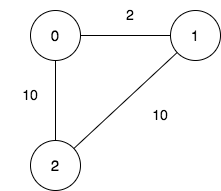
输入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出：5
解释：可行的关闭分部方案有：
- 关闭分部集合 [2] ，剩余分部为 [0,1] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 5 种可行的关闭方案。

示例 2：

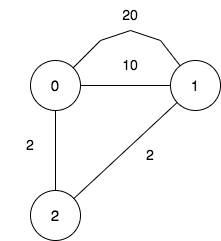
输入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出：7
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0,1,2] ，它们之间的最远距离为 4 。
- 关闭分部集合 [0] ，剩余分部为 [1,2] ，它们之间的距离为 2 。
- 关闭分部集合 [1] ，剩余分部为 [0,2] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 7 种可行的关闭方案。

示例 3：

输入：n = 1, maxDistance = 10, roads = []
输出：2
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0] 。
- 关闭分部集合 [0] ，关闭后没有剩余分部。
总共有 2 种可行的关闭方案。

提示：

• 1 <= n <= 10
• $1 <= maxDistance <= 10^5$
• 0 <= roads.length <= 1000
• roads[i].length == 3
• 0 <= ui, vi <= n - 1
• ui != vi
• 1 <= wi <= 1000
• 一开始所有分部之间通过道路互相可以到达。

分析

有条件的最短路

二进制枚举 + Floyd

class Solution {
    public int numberOfSets(int n, int maxDistance, int[][] roads) {
        int[][] g = new int[n][n];
        for (int[] row : g) {
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        }

        for (int[] e : roads) {
            int x = e[0];
            int y = e[1];
            int wt = e[2];
            g[x][y] = Math.min(g[x][y], wt);
            g[y][x] = Math.min(g[y][x], wt);
        }

        int ans = 0;
        int[][] f = new int[n][n];
        next:
        for (int s = 0;s < (1 << n);s++) {
            for (int i = 0;i < n;i++) {
                if ((s >> i & 1) == 1) {
                    System.arraycopy(g[i], 0 , f[i], 0, n);
                }
            }

            // folyd
            for(int k = 0;k < n;k++) {
                if ((s >> k & 1) == 0) {
                    continue;
                }
                for (int i = 0;i < n;i++) {
                    if ((s >> i & 1) == 0) {
                        continue;
                    }
                    for (int j = 0;j < n;j++) {
                        f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j]);
                    }
                }
            }
            // 判断保留的节点之间的最短路是否均不超过 maxDistance
            for (int i = 0;i < n;i++) {
                if ((s >> i & 1) == 0) {
                    continue;
                }
                for (int j = 0;j < i;j++) {
                    if ((s >> j & 1) == 1 && f[i][j] > maxDistance) {
                        continue next;
                    }
                }
            }
            ans++;
        }
        return ans;
    }
}

状压 DP + Floyd

class Solution {
    public int numberOfSets(int n, int maxDistance, int[][] roads) {
        int[][] g = new int[n][n];
        for (int[] row : g) {
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        }
        for (int[] e : roads) {
            int x = e[0];
            int y = e[1];
            int wt = e[2];
            g[x][y] = Math.min(g[x][y], wt);
            g[y][x] = Math.min(g[y][x], wt);
        }

        int ans = 1; // s=0 一定满足要求
        int[][][] f = new int[1 << n][n][n];
        for (int[][] matrix : f) {
            for (int[] row : matrix) {
                Arrays.fill(row, Integer.MAX_VALUE / 2);
            }
        }
        f[0] = g;
        for (int s = 1; s < (1 << n); s++) {
            int k = Integer.numberOfTrailingZeros(s);
            int t = s ^ (1 << k);
            boolean ok = true;
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    f[s][i][j] = Math.min(f[t][i][j], f[t][i][k] + f[t][k][j]);
                    if (ok && j < i && (s >> i & 1) != 0 && (s >> j & 1) != 0 && f[s][i][j] > maxDistance) {
                        ok = false;
                    }
                }
            }
            ans += ok ? 1 : 0;
        }
        return ans;
    }
}

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1056615746@qq.com