题目
给你一个二维数组 edges 表示一个 n 个点的无向图,其中 $edges[i] = [u_i, v_i, length_i]$ 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。
同时给你一个数组 disappear ,其中 disappear[i] 表示节点 i 从图中消失的时间点,在那一刻及以后,你无法再访问这个节点。
注意,图有可能一开始是不连通的,两个节点之间也可能有多条边。
请你返回数组 answer ,answer[i] 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点 i ,那么 answer[i] 为 -1 。
示例 1:
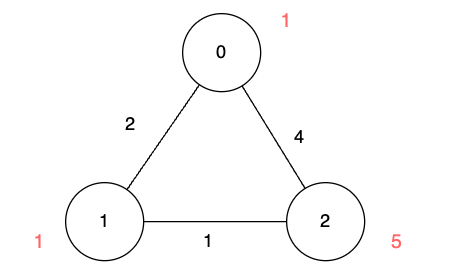
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]
输出:[0,-1,4]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。但当我们到达的时候,它已经消失了,所以我们无法到达它。
对于节点 2 ,我们需要至少 4 单位时间,通过 edges[2] 到达。
示例 2:
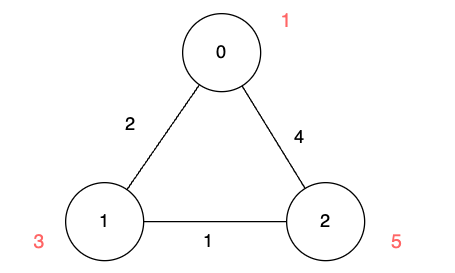
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]
输出:[0,2,3]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。
对于节点 2 ,我们需要至少 3 单位时间,通过 edges[0] 和 edges[1] 到达。
示例 3:
输入:n = 2, edges = [[0,1,1]], disappear = [1,1]
输出:[0,-1]
解释:
当我们到达节点 1 的时候,它恰好消失,所以我们无法到达节点 1 。
提示:
- $1 <= n <= 5 * 10^4$
- $0 <= edges.length <= 10^5$
- $edges[i] == [u_i, v_i, length_i]$
- $0 <= u_i, v_i <= n - 1$
- $1 <= lengthi <= 10^5$
disappear.length == n- $1 <= disappear[i] <= 10^5$
分析
求0节点到图(图中的边会消失,需要在消失之间路过,尽可能的利用)中其他所有节点的最短时间.
class Solution {
public int[] minimumTime(int n, int[][] edges, int[] disappear) {
// 稀疏图用邻接表
List<int[]>[] g = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int[] e : edges) {
int x = e[0];
int y = e[1];
int wt = e[2];
g[x].add(new int[]{y, wt});
g[y].add(new int[]{x, wt});
}
int[] dis = new int[n];
Arrays.fill(dis, -1);
dis[0] = 0;
// 优先队列 广度优先遍历
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> (a[0] - b[0]));
pq.offer(new int[]{0,0});
while(!pq.isEmpty()) {
int[] p = pq.poll();
int dx = p[0];
int x = p[1];
if (dx > dis[x]) {
continue;
}
for (int[] e : g[x]) {
int y = e[0];
int newDis = dx + e[1];
if (newDis < disappear[y] && (dis[y] < 0 || newDis < dis[y])) {
dis[y] = newDis;
pq.offer(new int[]{newDis, y});
}
}
}
return dis;
}
}
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1056615746@qq.com

